7 Hằng Đẳng Thức Đáng Nhớ Lớp 8 Kết Nối Tri Thức


Chính Sách Vận Chuyển Và Đổi Trả Hàng
Miễn phí vận chuyển mọi đơn hàng từ 500K
- Phí ship mặc trong nước 50K
- Thời gian nhận hàng 2-3 ngày trong tuần
- Giao hàng hỏa tốc trong 24h
- Hoàn trả hàng trong 30 ngày nếu không hài lòng
Mô tả sản phẩm
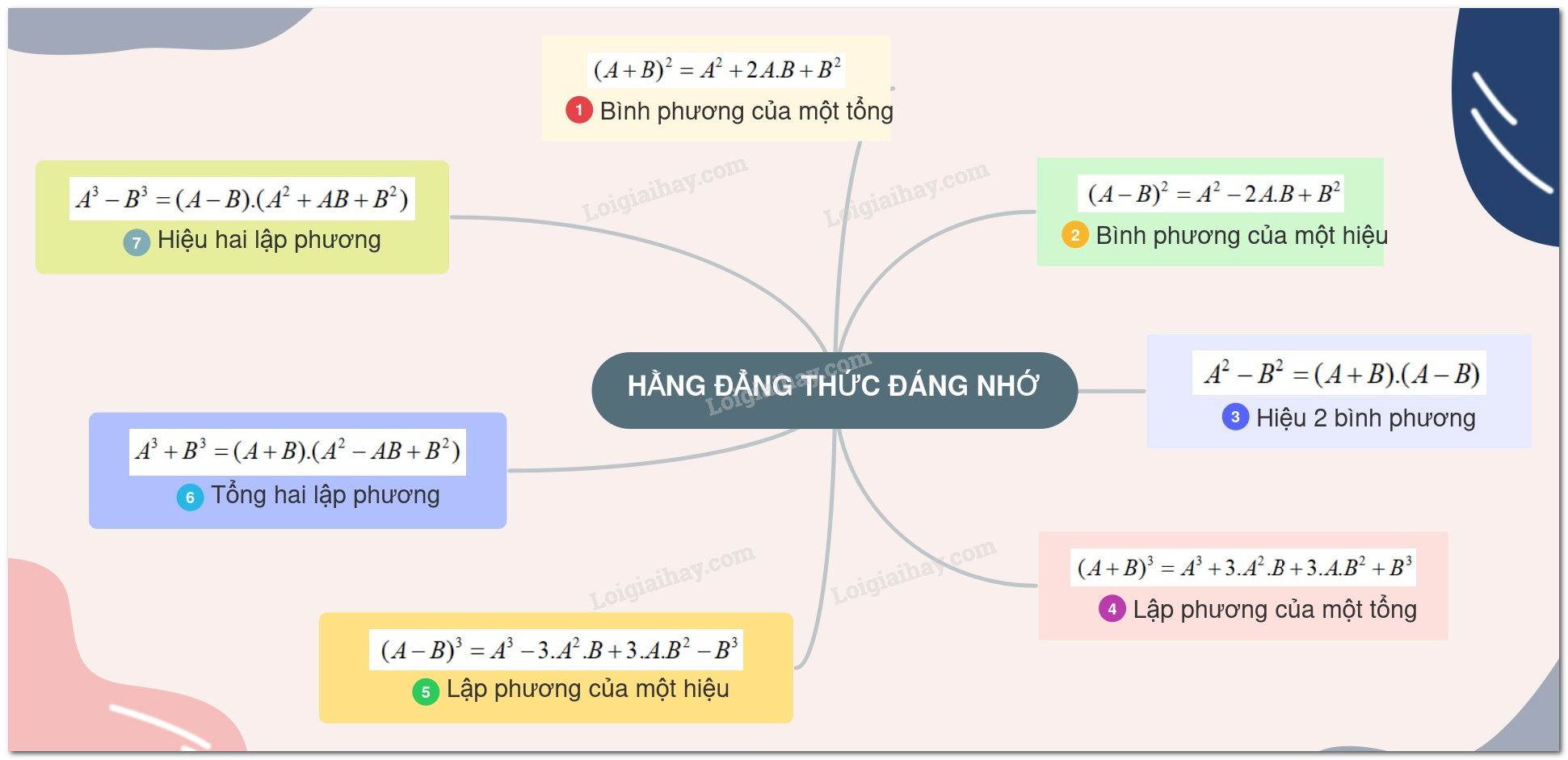
7 hằng đẳng thức đáng nhớ lớp 8 trong chương trình Kết nối tri thức gồm: bình phương của một tổng, bình phương của một hiệu, hiệu hai bình phương, lập phương của một tổng, lập phương của một hiệu, tổng hai lập phương và hiệu hai lập phương. Việc nắm vững các hằng đẳng thức này là cực kỳ quan trọng để giải quyết các bài toán đại số, rút gọn biểu thức và giải phương trình hiệu quả.
Bình Phương của một Tổng và Hiệu
Bình phương của một tổng: (A + B)² = A² + 2AB + B²
Công thức này thể hiện rằng bình phương của tổng hai biểu thức bằng bình phương của biểu thức thứ nhất cộng với hai lần tích của hai biểu thức đó cộng với bình phương của biểu thức thứ hai.
Bình phương của một hiệu: (A - B)² = A² - 2AB + B²
Tương tự, bình phương của hiệu hai biểu thức bằng bình phương của biểu thức thứ nhất trừ đi hai lần tích của hai biểu thức đó cộng với bình phương của biểu thức thứ hai.
Hiệu Hai Bình Phương
Hiệu hai bình phương: A² - B² = (A + B)(A - B)
Công thức này cho phép phân tích một hiệu hai bình phương thành tích của tổng và hiệu của hai biểu thức.
Lập Phương của một Tổng và Hiệu
Lập phương của một tổng: (A + B)³ = A³ + 3A²B + 3AB² + B³
Lập phương của tổng hai biểu thức được khai triển thành tổng của lập phương biểu thức thứ nhất, ba lần bình phương biểu thức thứ nhất nhân với biểu thức thứ hai, ba lần biểu thức thứ nhất nhân bình phương biểu thức thứ hai và lập phương biểu thức thứ hai.
Lập phương của một hiệu: (A - B)³ = A³ - 3A²B + 3AB² - B³
Tương tự, lập phương của hiệu hai biểu thức được khai triển thành tổng của lập phương biểu thức thứ nhất, trừ đi ba lần bình phương biểu thức thứ nhất nhân với biểu thức thứ hai, cộng với ba lần biểu thức thứ nhất nhân bình phương biểu thức thứ hai và trừ đi lập phương biểu thức thứ hai.
Tổng và Hiệu Hai Lập Phương
Tổng hai lập phương: A³ + B³ = (A + B)(A² - AB + B²)
Công thức này giúp phân tích tổng hai lập phương thành tích của tổng hai biểu thức với một tam thức bậc hai.
Hiệu hai lập phương: A³ - B³ = (A - B)(A² + AB + B²)
Công thức này giúp phân tích hiệu hai lập phương thành tích của hiệu hai biểu thức với một tam thức bậc hai.
Sản phẩm hữu ích: công thức phủ định
Sản phẩm liên quan: bài 1 thần thoại và sử thi
Sản phẩm hữu ích: mặt nạ siêu nhân gao
Sản phẩm hữu ích: thể tích hình hộp lập phương
Sản phẩm hữu ích: cách chuyển km/h sang m/s