Công thức phủ định trong toán học

Mô tả sản phẩm

Công thức phủ định trong toán học dùng để biểu diễn mệnh đề phủ định của một mệnh đề cho trước. Nói cách khác, nó cho ta biết điều kiện nào làm cho một mệnh đề trở nên sai.

Mệnh đề và Phủ định

Khái niệm mệnh đề

Một mệnh đề là một câu khẳng định có thể xác định được tính đúng sai. Ví dụ: "2 + 2 = 4" là một mệnh đề đúng, trong khi "Trời hôm nay mưa" là một mệnh đề, có thể đúng hoặc sai tùy thuộc vào thời tiết thực tế.

Phủ định của một mệnh đề

Phủ định của một mệnh đề P, ký hiệu là ¬P (hoặc P'), là một mệnh đề mới, có giá trị đúng sai ngược lại với P. Nếu P đúng thì ¬P sai, và ngược lại, nếu P sai thì ¬P đúng. Ví dụ: Nếu P là "2 + 2 = 4" (đúng), thì ¬P là "2 + 2 ≠ 4" (sai). Nếu Q là "Trời hôm nay nắng" (giả sử đúng), thì ¬Q là "Trời hôm nay không nắng" (sai).

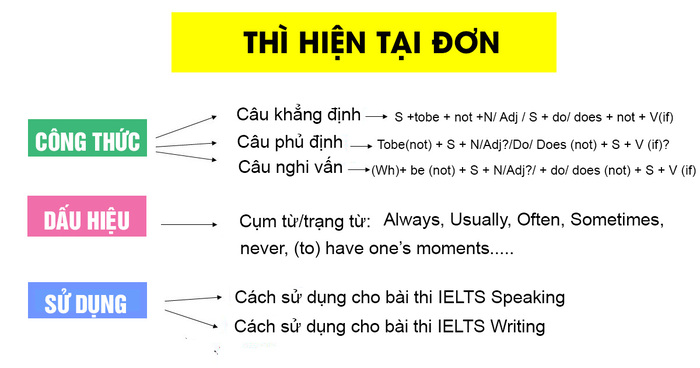
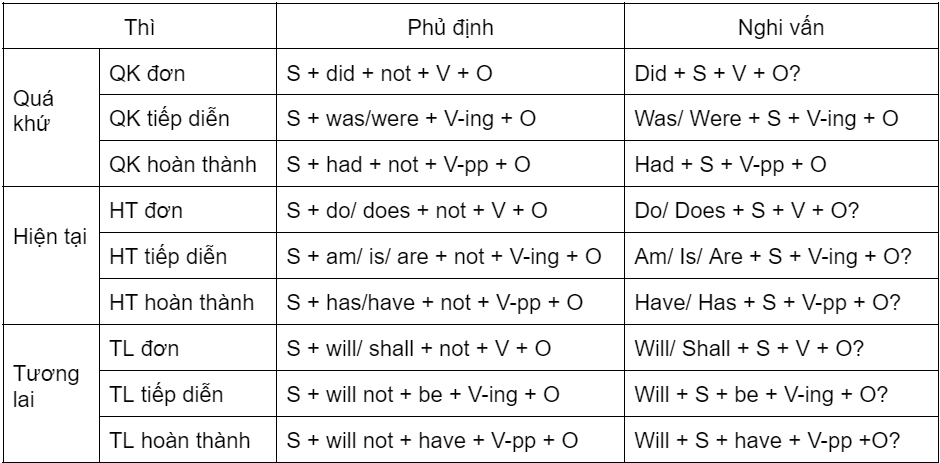
Các dạng công thức phủ định

Phủ định của mệnh đề đơn giản

Phủ định của một mệnh đề đơn giản thường được thực hiện bằng cách thêm từ "không" hoặc "không phải" vào trước mệnh đề đó, hoặc sử dụng các từ ngữ tương đương để đảo ngược ý nghĩa. Ví dụ: Phủ định của "x > 5" là "x ≤ 5".

Phủ định của mệnh đề phức hợp

Với mệnh đề phức hợp (sử dụng các liên từ như "và", "hoặc", "nếu...thì"), việc phủ định phức tạp hơn. Ta cần áp dụng các quy tắc De Morgan:

• ¬(P ∧ Q) ≡ (¬P ∨ ¬Q)
• ¬(P ∨ Q) ≡ (¬P ∧ ¬Q)
• ¬(P → Q) ≡ (P ∧ ¬Q)

Trong đó:

• ∧: ký hiệu "và"
• ∨: ký hiệu "hoặc"
• →: ký hiệu "nếu...thì"
• ≡: ký hiệu "tương đương"

Các quy tắc này cho phép ta phân tích và viết lại mệnh đề phủ định một cách chính xác.

Ứng dụng của công thức phủ định

Công thức phủ định có ứng dụng rộng rãi trong toán học, logic học và khoa học máy tính. Nó giúp ta chứng minh định lý, giải quyết bài toán, và đặc biệt quan trọng trong lập trình khi cần xử lý các điều kiện logic phức tạp.

Xem thêm: điểm giống nhau về khí hậu của duyên hải nam trung bộ và tây nguyên là

Sản phẩm hữu ích: than hoạt tính công thức hóa học

Xem thêm: quay len chi hang xom

Xem thêm: hình nền đen thui