Xác suất của biến cố lớp 10


Chính Sách Vận Chuyển Và Đổi Trả Hàng
Miễn phí vận chuyển mọi đơn hàng từ 500K
- Phí ship mặc trong nước 50K
- Thời gian nhận hàng 2-3 ngày trong tuần
- Giao hàng hỏa tốc trong 24h
- Hoàn trả hàng trong 30 ngày nếu không hài lòng
Mô tả sản phẩm
Xác suất của một biến cố trong chương trình toán lớp 10 được định nghĩa là tỷ lệ giữa số phần tử của biến cố đó và số phần tử của không gian mẫu. Bài viết này sẽ giúp bạn hiểu rõ hơn về khái niệm này cùng với các công thức và ví dụ minh họa.
Khái niệm cơ bản về xác suất của biến cố
Không gian mẫu và biến cố
Không gian mẫu Ω là tập hợp tất cả các kết quả có thể xảy ra của một phép thử. Biến cố A là một tập con của không gian mẫu, ký hiệu là A ⊂ Ω. Ví dụ: Khi tung một con xúc xắc, không gian mẫu là Ω = {1, 2, 3, 4, 5, 6}. Biến cố A: "xuất hiện mặt chẵn" là A = {2, 4, 6}.Xác suất của biến cố
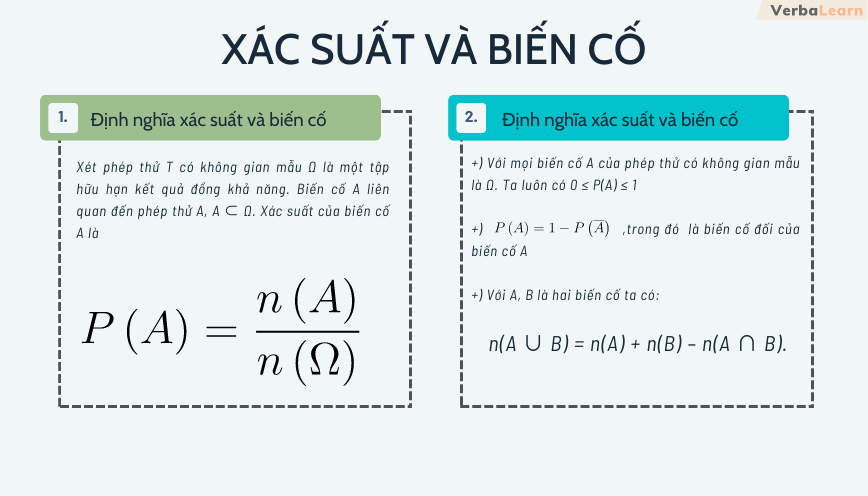
Xác suất của biến cố A, ký hiệu là P(A), được tính bằng tỷ lệ giữa số phần tử của biến cố A và số phần tử của không gian mẫu Ω: P(A) = n(A) / n(Ω) Với n(A) là số phần tử của biến cố A và n(Ω) là số phần tử của không gian mẫu Ω. Xác suất luôn nằm trong khoảng [0, 1]. P(A) = 0 nghĩa là biến cố A không thể xảy ra, P(A) = 1 nghĩa là biến cố A chắc chắn xảy ra.Các loại biến cố và tính chất
Biến cố đối
Biến cố đối của biến cố A, ký hiệu là Ac hoặc A-, là tập hợp các phần tử thuộc không gian mẫu nhưng không thuộc A. Ta có: P(A) + P(Ac) = 1.Biến cố hợp và giao
Nếu A và B là hai biến cố, thì: * Biến cố hợp A ∪ B là biến cố xảy ra ít nhất một trong hai biến cố A hoặc B. * Biến cố giao A ∩ B là biến cố xảy ra cả hai biến cố A và B.Biến cố độc lập
Hai biến cố A và B được gọi là độc lập nếu việc xảy ra của biến cố này không ảnh hưởng đến xác suất xảy ra của biến cố kia. Nếu A và B độc lập, thì P(A ∩ B) = P(A) * P(B).Ví dụ minh họa
Giả sử ta tung một đồng xu hai lần. Không gian mẫu là Ω = {SS, SN, NS, NN} (S: sấp, N: ngửa). Tính xác suất của biến cố A: "xuất hiện ít nhất một mặt sấp". Biến cố A = {SS, SN, NS}. Vậy n(A) = 3, n(Ω) = 4. P(A) = n(A) / n(Ω) = 3/4 = 0.75Sản phẩm liên quan: dê tươi vĩnh lộc 5
Sản phẩm liên quan: 2 lít nước là bao nhiêu ml
Sản phẩm liên quan: bút kẻ mắt lâu trôi
Sản phẩm hữu ích: nhặt được dây chuyền vàng đánh con gì
Sản phẩm hữu ích: giới hạn đo của một thước là