Viết Phương Trình Tiếp Tuyến Của Đường Tròn

Mô tả sản phẩm

Viết phương trình tiếp tuyến của đường tròn là một bài toán quen thuộc trong hình học giải tích. Để viết được phương trình tiếp tuyến, ta cần biết tọa độ điểm tiếp xúc và phương trình đường tròn. Có nhiều cách để giải quyết bài toán này, tùy thuộc vào dữ kiện đã cho.

Các trường hợp viết phương trình tiếp tuyến

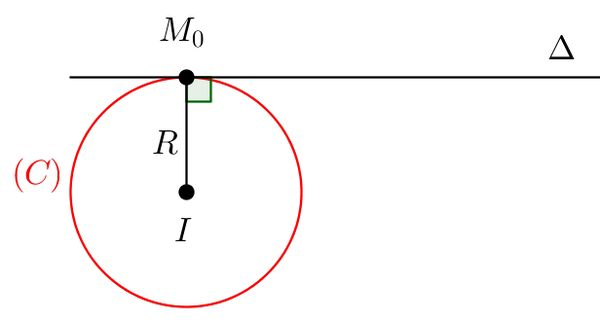
Trường hợp 1: Biết tọa độ điểm tiếp xúc và phương trình đường tròn

Giả sử đường tròn có phương trình (x-a)² + (y-b)² = r² và điểm tiếp xúc là M(x₀, y₀). Phương trình tiếp tuyến tại M có dạng: (x₀ - a)(x - a) + (y₀ - b)(y - b) = r².

Trường hợp 2: Biết phương trình đường tròn và hệ số góc của tiếp tuyến

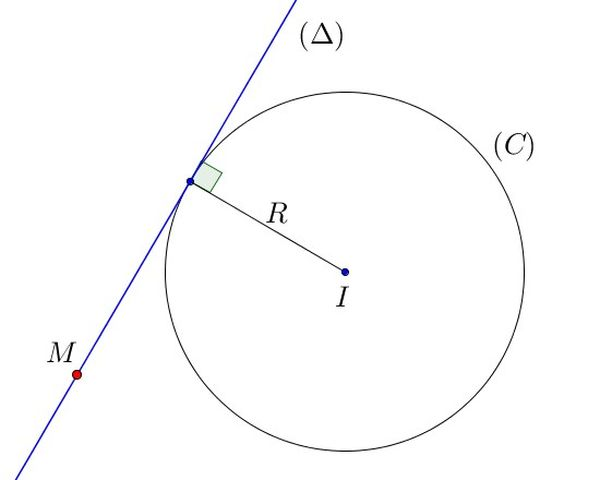
Giả sử đường tròn có phương trình x² + y² + 2ax + 2by + c = 0 và tiếp tuyến có hệ số góc k. Ta thay y = k(x-x₀)+y₀ vào phương trình đường tròn. Vì tiếp tuyến chỉ cắt đường tròn tại một điểm, nên phương trình bậc hai thu được sẽ có nghiệm kép. Điều kiện để có nghiệm kép là delta = 0. Từ đó ta tìm được x₀ và y₀, rồi suy ra phương trình tiếp tuyến.

Trường hợp 3: Biết phương trình đường tròn và tọa độ điểm nằm ngoài đường tròn

Giả sử đường tròn có phương trình (x-a)² + (y-b)² = r² và điểm A(x₁, y₁) nằm ngoài đường tròn. Phương trình tiếp tuyến đi qua A có dạng: (x-a)(x₁-a) + (y-b)(y₁-b) = r². Chú ý rằng từ điểm A ta có thể kẻ được hai tiếp tuyến đến đường tròn. Việc lựa chọn phương pháp phụ thuộc vào dữ kiện bài toán. Hiểu rõ các trường hợp trên sẽ giúp bạn giải quyết mọi bài toán viết phương trình tiếp tuyến của đường tròn một cách hiệu quả. Hãy luyện tập nhiều bài tập để nắm vững kiến thức này.

Xem thêm: các diện tích hình học

Sản phẩm liên quan: đặc điểm của thiên nhiên nhiệt đới ẩm gió mùa của nước ta là do

Sản phẩm liên quan: công chúa tóc mây tiếng anh là gì