Khai triển (x-y)^5 theo công thức nhị thức Newton
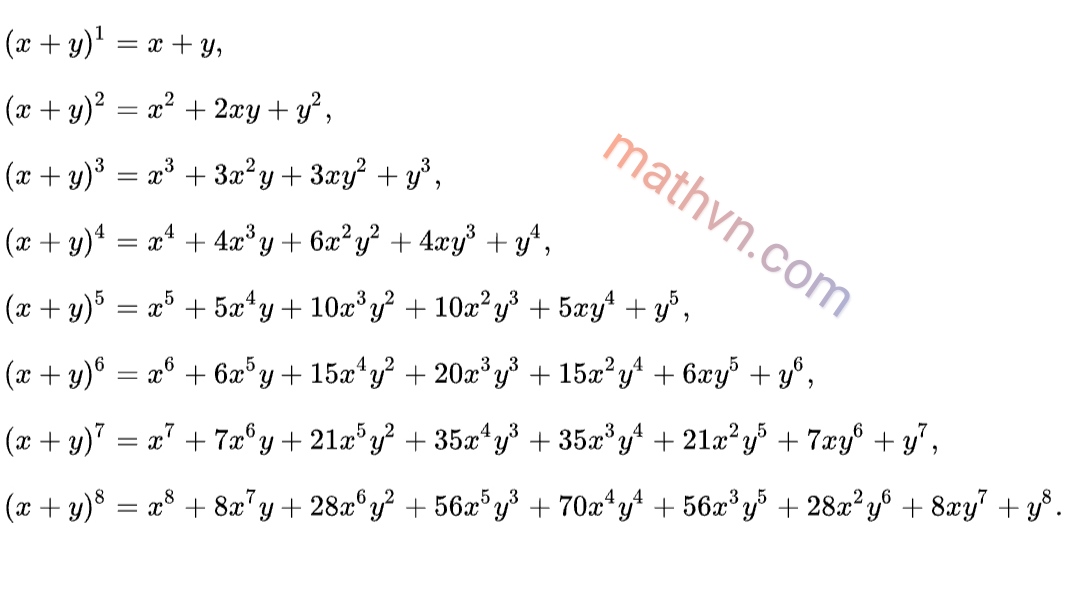
Chính Sách Vận Chuyển Và Đổi Trả Hàng
Miễn phí vận chuyển mọi đơn hàng từ 500K
- Phí ship mặc trong nước 50K
- Thời gian nhận hàng 2-3 ngày trong tuần
- Giao hàng hỏa tốc trong 24h
- Hoàn trả hàng trong 30 ngày nếu không hài lòng
Mô tả sản phẩm
Khai triển (x-y)5 theo công thức nhị thức Newton sẽ cho kết quả là x5 - 5x4y + 10x3y2 - 10x2y3 + 5xy4 - y5. Bài viết này sẽ hướng dẫn bạn cách khai triển biểu thức này một cách chi tiết.
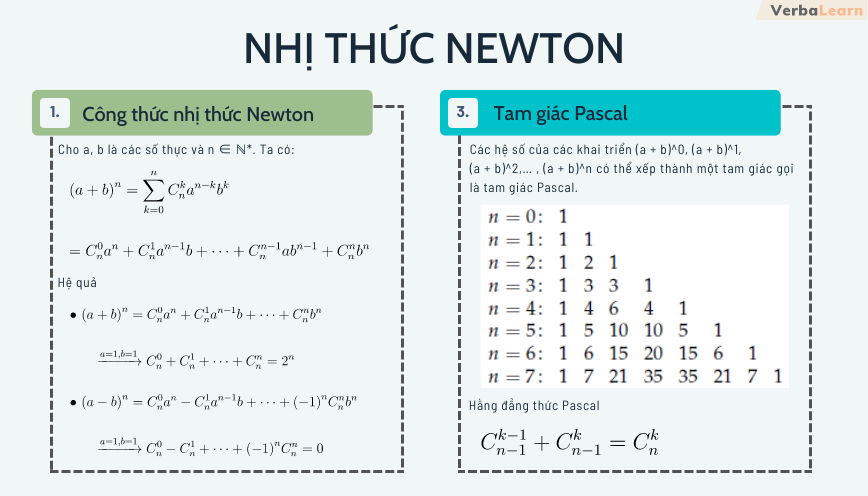
Công thức nhị thức Newton
Định nghĩa
Công thức nhị thức Newton là một công thức toán học cho phép khai triển lũy thừa của một tổng (hoặc hiệu) của hai số hạng. Công thức tổng quát được viết như sau: (a + b)n = Σ (nCk) * a(n-k) * bk, với k chạy từ 0 đến n, và nCk là tổ hợp chập k của n phần tử (n! / (k! * (n-k)!)).Áp dụng vào (x-y)5
Trong trường hợp (x-y)5, ta có a = x, b = -y và n = 5. Áp dụng công thức nhị thức Newton, ta có: (x - y)5 = Σ (5Ck) * x(5-k) * (-y)k, với k chạy từ 0 đến 5. Khai triển từng số hạng:- k = 0: (5C0) * x5 * (-y)0 = 1 * x5 * 1 = x5
- k = 1: (5C1) * x4 * (-y)1 = 5 * x4 * (-y) = -5x4y
- k = 2: (5C2) * x3 * (-y)2 = 10 * x3 * y2 = 10x3y2
- k = 3: (5C3) * x2 * (-y)3 = 10 * x2 * (-y3) = -10x2y3
- k = 4: (5C4) * x1 * (-y)4 = 5 * x * y4 = 5xy4
- k = 5: (5C5) * x0 * (-y)5 = 1 * 1 * (-y5) = -y5
Ứng dụng của công thức nhị thức Newton
Công thức nhị thức Newton có rất nhiều ứng dụng trong toán học, đặc biệt trong các lĩnh vực như giải tích, xác suất thống kê và đại số. Nó giúp đơn giản hóa việc tính toán các lũy thừa của đa thức và giải quyết các bài toán liên quan đến tổ hợp.Xem thêm: truyện ma căn nhà số 24
Sản phẩm liên quan: dấu ngoặc vuông trong toán học
Xem thêm: hiện tượng cảm ứng điện từ là hiện tượng