Ví dụ về Phương pháp Giải quyết Vấn đề ở Tiểu học
Chính Sách Vận Chuyển Và Đổi Trả Hàng
Miễn phí vận chuyển mọi đơn hàng từ 500K
- Phí ship mặc trong nước 50K
- Thời gian nhận hàng 2-3 ngày trong tuần
- Giao hàng hỏa tốc trong 24h
- Hoàn trả hàng trong 30 ngày nếu không hài lòng
Mô tả sản phẩm
Có rất nhiều phương pháp giúp học sinh tiểu học giải quyết vấn đề hiệu quả. Ví dụ, một bài toán về cộng trừ đơn giản có thể được giải quyết bằng cách vẽ hình minh họa hoặc sử dụng các vật dụng thực tế để mô phỏng bài toán. Một bài toán phức tạp hơn đòi hỏi sự phân tích từng bước và áp dụng các chiến lược giải quyết vấn đề.
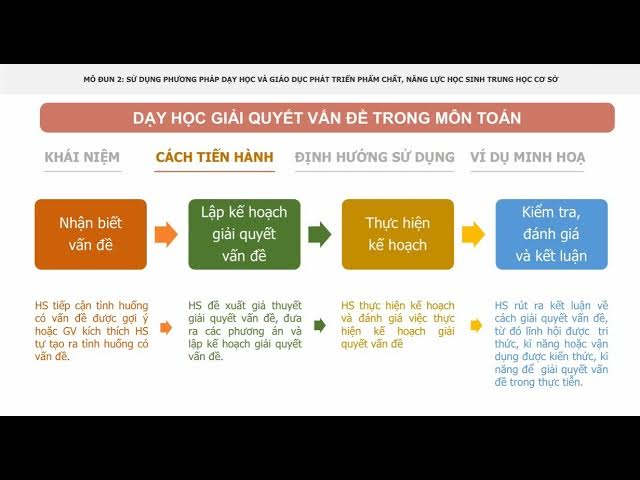
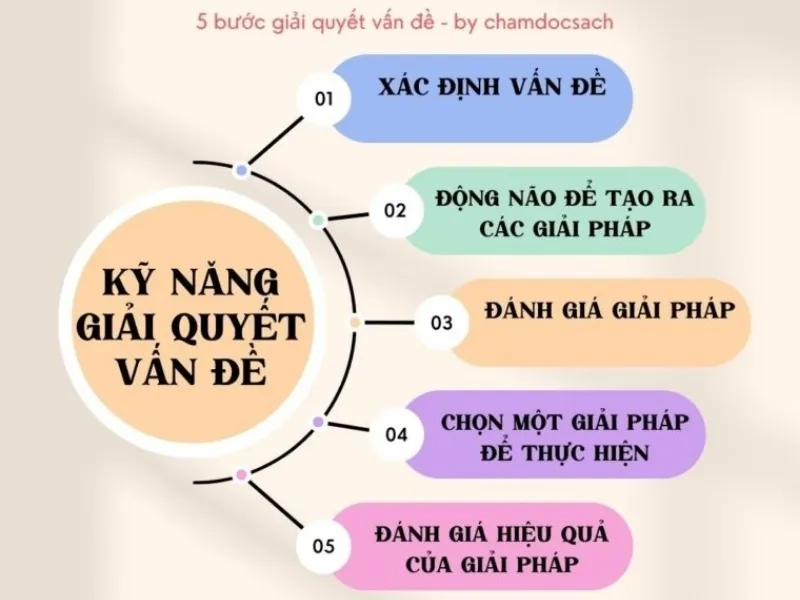
Các Phương Pháp Giải Quyết Vấn Đề Phổ Biến
Phương pháp vẽ hình minh họa
Giả sử bài toán: "Lan có 5 quả táo, mẹ cho Lan thêm 3 quả táo. Hỏi Lan có tất cả bao nhiêu quả táo?" Học sinh có thể vẽ 5 quả táo, sau đó vẽ thêm 3 quả táo nữa và đếm tổng số quả táo. Phương pháp này trực quan và dễ hiểu, đặc biệt hữu ích cho học sinh tiểu học đang làm quen với toán học.Phương pháp sử dụng vật dụng thực tế
Với bài toán trên, học sinh có thể dùng 5 viên bi đại diện cho 5 quả táo, sau đó thêm 3 viên bi nữa và đếm tổng số viên bi. Việc sử dụng vật dụng thực tế giúp học sinh dễ dàng hình dung bài toán và tìm ra đáp án chính xác.Phương pháp phân tích từng bước
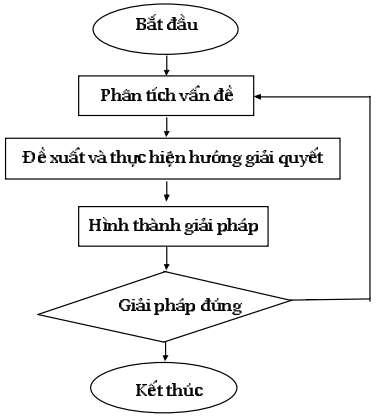
Đối với bài toán phức tạp hơn, chẳng hạn: "Một cửa hàng có 12 chiếc xe đạp, buổi sáng bán được 5 chiếc, buổi chiều bán được 3 chiếc. Hỏi cửa hàng còn lại bao nhiêu chiếc xe đạp?" Học sinh cần phân tích từng bước:- Bước 1: Tính tổng số xe đạp đã bán: 5 + 3 = 8 (chiếc)
- Bước 2: Tính số xe đạp còn lại: 12 - 8 = 4 (chiếc)
Phương pháp lập bảng
Một số bài toán có thể được giải quyết hiệu quả bằng cách lập bảng. Ví dụ, bài toán so sánh số lượng đồ vật khác nhau. Việc lập bảng giúp sắp xếp thông tin một cách có hệ thống và dễ dàng so sánh.Phương pháp thử và sai
Đây là phương pháp hữu ích khi học sinh không biết bắt đầu từ đâu. Học sinh có thể thử nhiều cách khác nhau cho đến khi tìm ra đáp án đúng. Tuy nhiên, phương pháp này cần được kết hợp với sự suy luận logic để tránh mất nhiều thời gian. Việc lựa chọn phương pháp giải quyết vấn đề phù hợp phụ thuộc vào từng bài toán cụ thể và khả năng của từng học sinh. Quan trọng là khuyến khích học sinh tự tin thử nghiệm và tìm ra cách giải tốt nhất cho mình.Sản phẩm liên quan: truyện ma duy ly
Xem thêm: truyện ngắn không có cốt truyện li kì hấp dẫn có thể là một truyện hay được không
Sản phẩm hữu ích: truyện tấm cám tác giả là ai
Sản phẩm liên quan: tuyển tập thơ xuân quỳnh