Vecto Pháp Tuyến là gì?

Mô tả sản phẩm

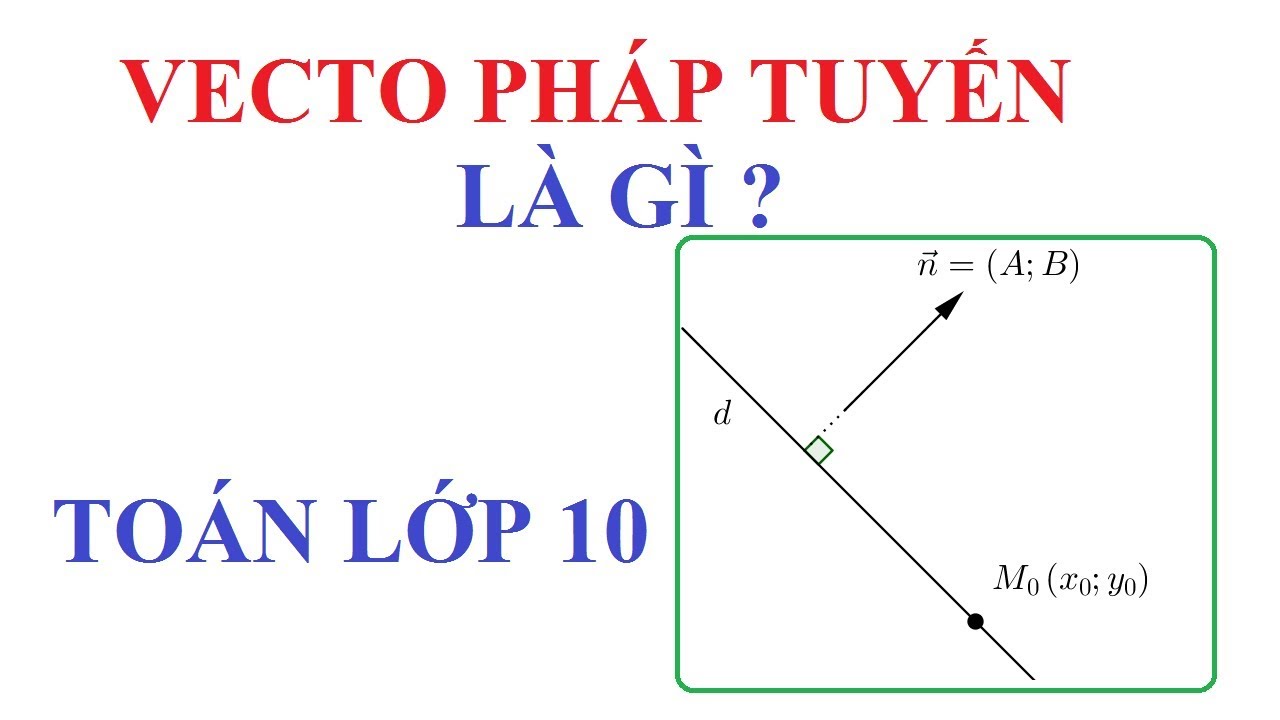
Vecto pháp tuyến là một vecto vuông góc với một đối tượng hình học, thường là một mặt phẳng hoặc một đường thẳng trong không gian. Nó đóng vai trò quan trọng trong việc xác định vị trí và tính chất của đối tượng đó.

Vecto Pháp Tuyến của Mặt Phẳng

Cách tìm vecto pháp tuyến của mặt phẳng

Để tìm vecto pháp tuyến của một mặt phẳng, ta cần biết ít nhất hai vecto nằm trên mặt phẳng đó. Sau đó, ta tính tích có hướng của hai vecto này. Kết quả chính là vecto pháp tuyến của mặt phẳng. Ví dụ, nếu hai vecto nằm trên mặt phẳng là a và b, thì vecto pháp tuyến n được tính bằng: n = a x b (ký hiệu x là phép tích có hướng). Lưu ý rằng vecto pháp tuyến không duy nhất, bất kỳ vecto nào cùng phương với n cũng là vecto pháp tuyến của mặt phẳng.

Ứng dụng của vecto pháp tuyến mặt phẳng

Vecto pháp tuyến của mặt phẳng được ứng dụng rộng rãi trong nhiều lĩnh vực, bao gồm: * Xác định phương trình mặt phẳng. * Tính góc giữa hai mặt phẳng. * Xác định khoảng cách từ một điểm đến một mặt phẳng. * Trong đồ họa máy tính 3D để biểu diễn và thao tác với các đối tượng hình học.

Vecto Pháp Tuyến của Đường Thẳng

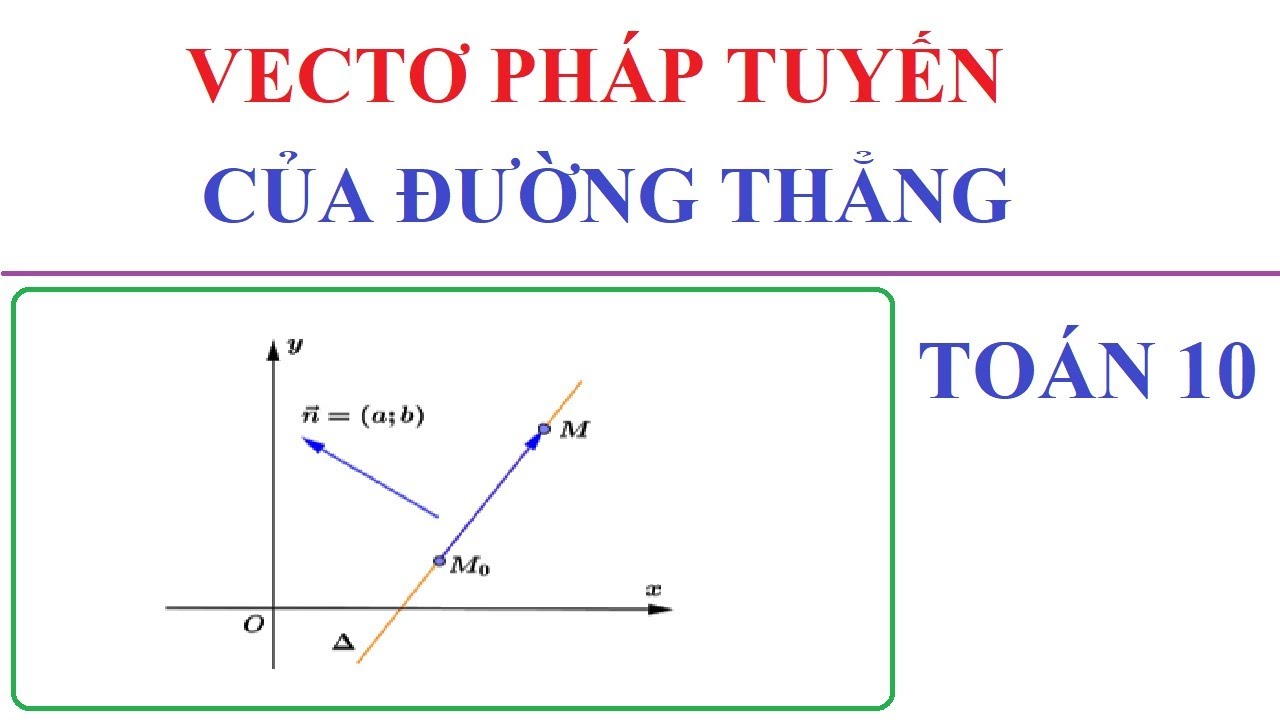
Cách tìm vecto pháp tuyến của đường thẳng

Vecto pháp tuyến của đường thẳng trong không gian là vecto vuông góc với đường thẳng đó. Nếu đường thẳng được cho bởi phương trình tham số, ta có thể tìm vecto chỉ phương của đường thẳng. Vecto pháp tuyến sẽ vuông góc với vecto chỉ phương này. Trong không gian 2 chiều, vecto pháp tuyến của đường thẳng ax + by + c = 0 là (a, b).

Ứng dụng của vecto pháp tuyến đường thẳng

Vecto pháp tuyến của đường thẳng được sử dụng để: * Xác định phương trình đường thẳng. * Tính góc giữa hai đường thẳng. * Xác định khoảng cách từ một điểm đến một đường thẳng.

Sản phẩm hữu ích: nêu các dạng của cơ năng

Sản phẩm hữu ích: số tương đối kết cấu

Xem thêm: cách tính chênh lệch