Vecto Chỉ Phương và Vecto Pháp Tuyến

Mô tả sản phẩm

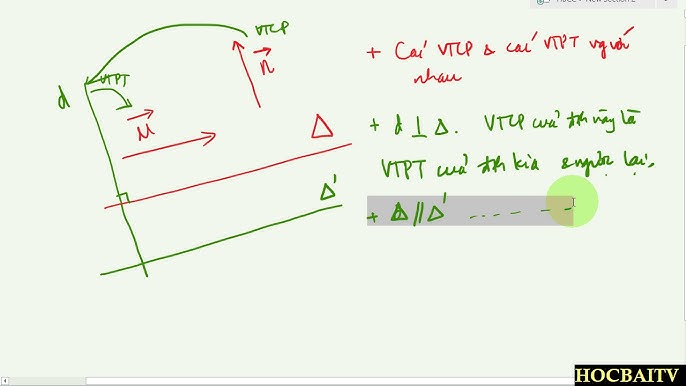
Vecto chỉ phương và vecto pháp tuyến là hai khái niệm quan trọng trong hình học không gian, dùng để xác định phương của đường thẳng và mặt phẳng. Vecto chỉ phương của đường thẳng là vecto cùng phương với đường thẳng đó, còn vecto pháp tuyến của mặt phẳng là vecto vuông góc với mặt phẳng đó. Cùng tìm hiểu chi tiết hơn về hai khái niệm này nhé!

Vecto Chỉ Phương

Định nghĩa Vecto Chỉ Phương

Vecto chỉ phương của đường thẳng là một vecto không suy biến, có phương song song hoặc trùng với phương của đường thẳng đó. Một đường thẳng có vô số vecto chỉ phương, chúng cùng phương với nhau. Nếu →a là vecto chỉ phương của đường thẳng d, thì k→a (k là số thực khác 0) cũng là vecto chỉ phương của d.

Ứng dụng của Vecto Chỉ Phương

Vecto chỉ phương được sử dụng rộng rãi trong việc xác định phương trình tham số và phương trình chính tắc của đường thẳng trong không gian. Việc hiểu rõ vecto chỉ phương giúp ta dễ dàng giải quyết các bài toán liên quan đến vị trí tương đối của các đường thẳng, góc giữa các đường thẳng, khoảng cách từ điểm đến đường thẳng, v.v…

Vecto Pháp Tuyến

Định nghĩa Vecto Pháp Tuyến

Vecto pháp tuyến của mặt phẳng là một vecto không suy biến, vuông góc với mặt phẳng đó. Tương tự như vecto chỉ phương, một mặt phẳng cũng có vô số vecto pháp tuyến, chúng cùng phương với nhau. Nếu →n là vecto pháp tuyến của mặt phẳng (P), thì k→n (k là số thực khác 0) cũng là vecto pháp tuyến của (P).

Ứng dụng của Vecto Pháp Tuyến

Vecto pháp tuyến đóng vai trò quan trọng trong việc xác định phương trình tổng quát của mặt phẳng. Nó giúp ta giải quyết các bài toán liên quan đến vị trí tương đối của các mặt phẳng, góc giữa các mặt phẳng, khoảng cách từ điểm đến mặt phẳng, vị trí tương đối giữa đường thẳng và mặt phẳng, v.v…

Xem thêm: các dạng bài tập tiếng việt lớp 2 kì 1

Sản phẩm liên quan: cánh đồng điện gió đầm nại

Sản phẩm hữu ích: quê tôi như thuở nào