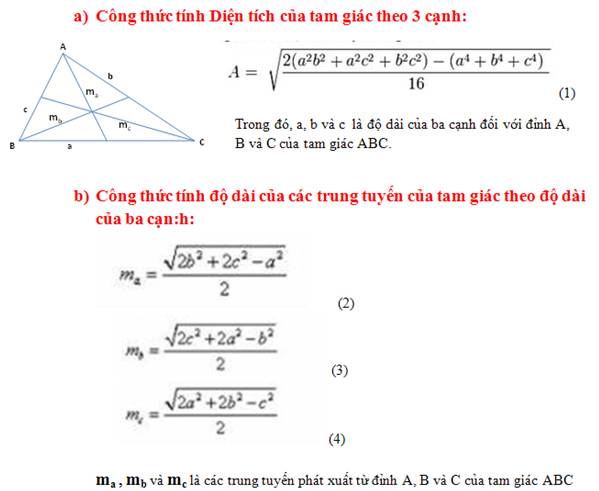
Trung tuyến trong tam giác đều

Mô tả sản phẩm

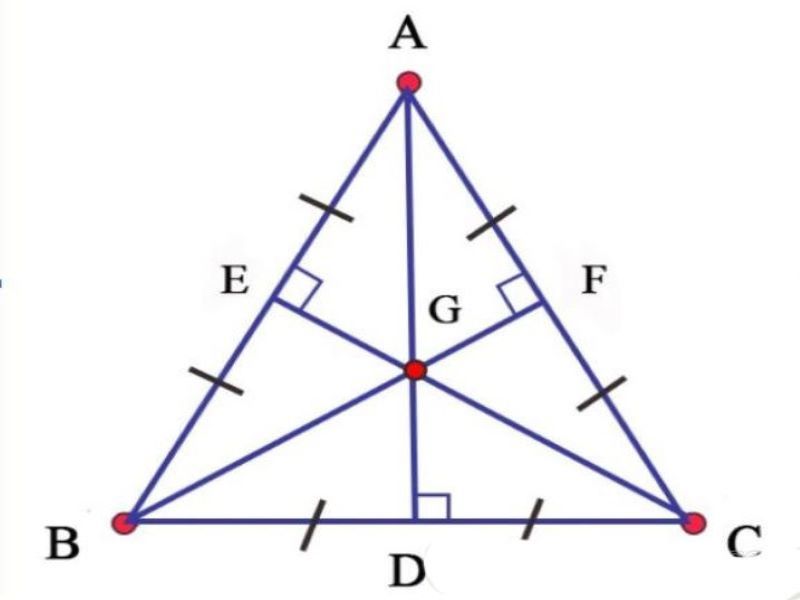
Trung tuyến trong tam giác đều chính là đường cao, đường phân giác, và đường trung trực của tam giác đó. Nó đồng thời cũng là trục đối xứng của tam giác. Do đó, trung tuyến chia tam giác đều thành hai tam giác vuông cân bằng nhau.

Tính chất của trung tuyến trong tam giác đều

Độ dài trung tuyến:

Nếu cạnh của tam giác đều là a, thì độ dài mỗi trung tuyến sẽ là a√3/2. Điều này có thể chứng minh dễ dàng bằng định lý Pytago trong tam giác vuông cân được tạo ra khi kẻ trung tuyến.

Giao điểm của các trung tuyến:

Ba trung tuyến của tam giác đều đồng quy tại một điểm gọi là trọng tâm. Trọng tâm này chia mỗi trung tuyến theo tỉ lệ 2:1, tính từ đỉnh đến đáy.

Ứng dụng:

Hiểu về tính chất trung tuyến trong tam giác đều giúp giải quyết nhiều bài toán hình học phức tạp hơn liên quan đến diện tích, chu vi, góc, và các yếu tố khác của tam giác. Ví dụ, ta có thể dễ dàng tính được diện tích của tam giác đều biết độ dài cạnh hoặc độ dài trung tuyến. Trung tuyến cũng đóng vai trò quan trọng trong việc xác định tâm đường tròn ngoại tiếp và nội tiếp của tam giác đều.

Sản phẩm liên quan: lực đàn hồi công thức

Sản phẩm hữu ích: thấu kính phân kì chỉ có khả năng cho

Sản phẩm hữu ích: bài tập tiếng anh lớp 3 theo từng unit có đáp an