Trung Trực Của Tam Giác

Mô tả sản phẩm

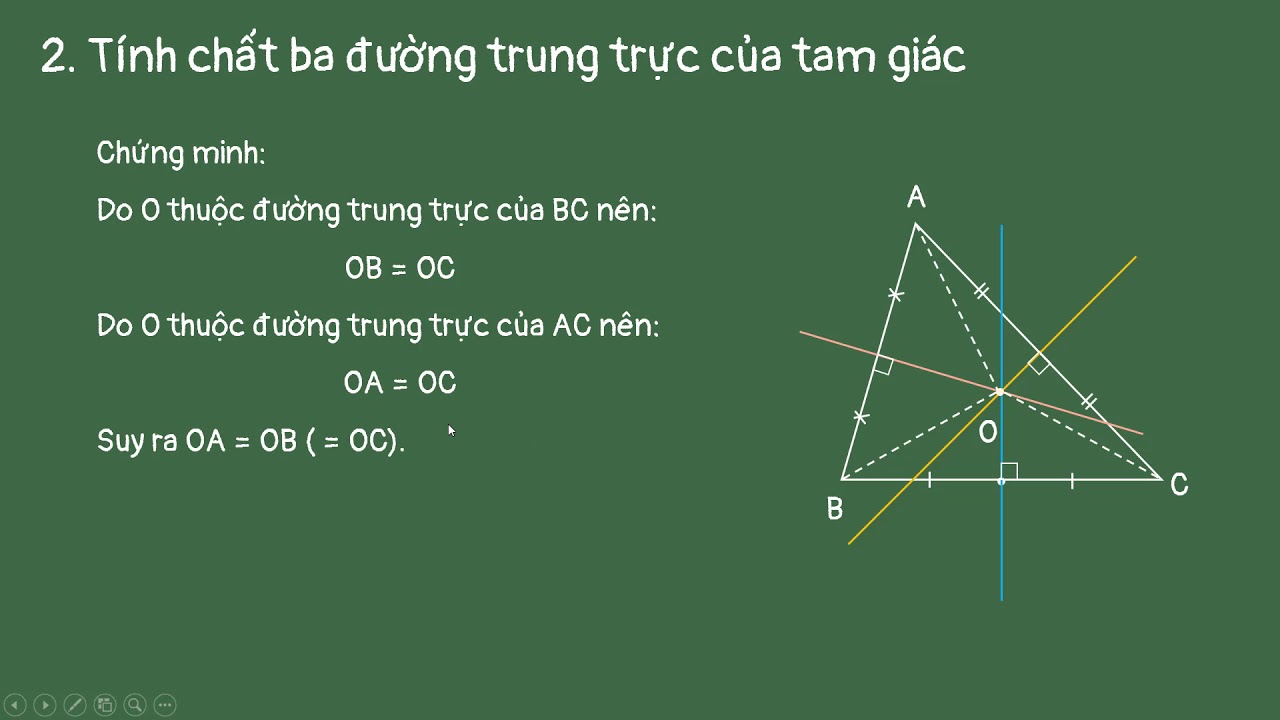
Trung trực của tam giác là đường thẳng vuông góc với một cạnh của tam giác tại trung điểm của cạnh đó. Mỗi tam giác có ba trung trực, một cho mỗi cạnh. Ba trung trực này đồng quy tại một điểm gọi là tâm đường tròn ngoại tiếp tam giác. Tâm đường tròn ngoại tiếp này cách đều ba đỉnh của tam giác.

Tính chất của trung trực tam giác

Định nghĩa:

Trung trực của một đoạn thẳng là đường thẳng vuông góc với đoạn thẳng đó tại trung điểm của nó. Trong tam giác, trung trực của mỗi cạnh là đường thẳng vuông góc với cạnh đó tại trung điểm của cạnh đó.

Tính chất đồng quy:

Ba đường trung trực của một tam giác luôn đồng quy tại một điểm. Điểm này gọi là tâm đường tròn ngoại tiếp tam giác.

Khoảng cách đến các đỉnh:

Tâm đường tròn ngoại tiếp (điểm giao của ba đường trung trực) cách đều ba đỉnh của tam giác. Khoảng cách này chính là bán kính của đường tròn ngoại tiếp.

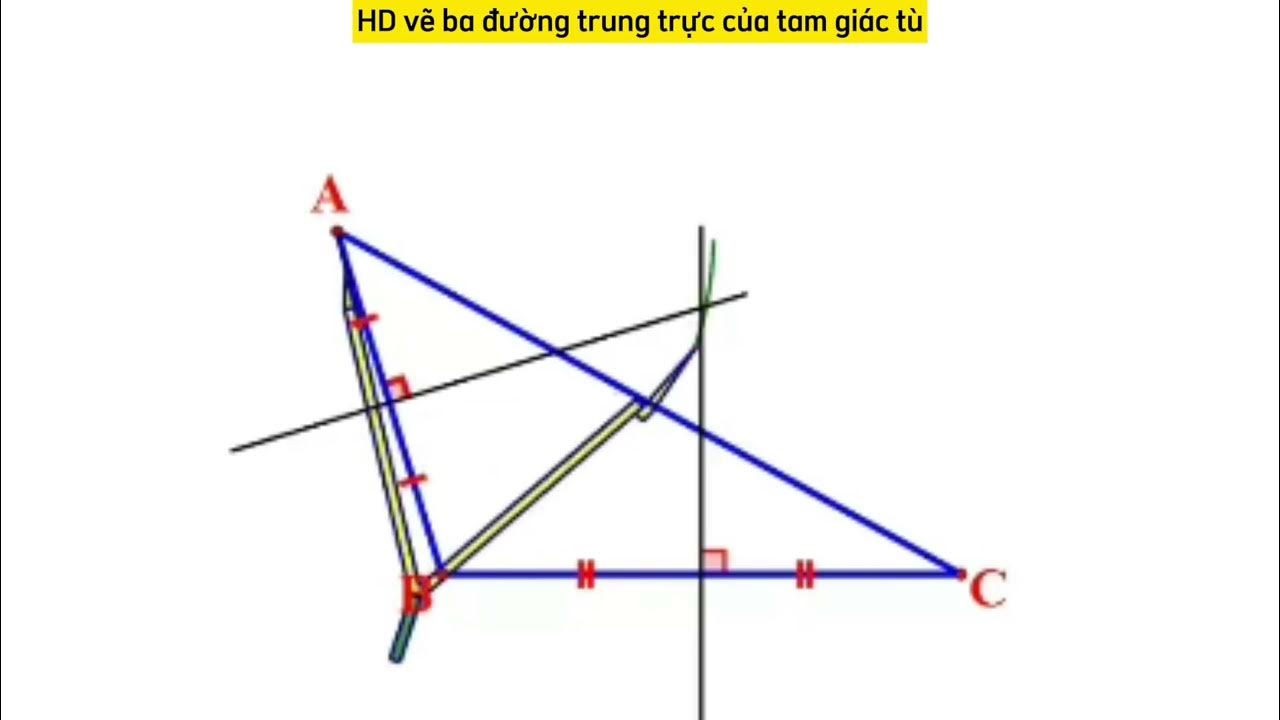
Cách vẽ trung trực của tam giác

Vẽ trung điểm:

Đầu tiên, xác định trung điểm của mỗi cạnh tam giác bằng cách dùng compa đo khoảng cách từ một đầu mút của cạnh đến đầu mút còn lại, sau đó đặt compa ở vị trí giữa, vẽ một cung tròn sao cho hai cung tròn giao nhau. Nối hai giao điểm của hai cung tròn lại, đường thẳng đó đi qua trung điểm của cạnh đó.

Vẽ đường vuông góc:

Từ trung điểm vừa tìm được, dùng êke hoặc compa để vẽ đường thẳng vuông góc với cạnh tam giác tại trung điểm đó. Đường thẳng này chính là đường trung trực của cạnh đó.

Tìm tâm đường tròn ngoại tiếp:

Vẽ ba đường trung trực của ba cạnh tam giác. Điểm giao của ba đường trung trực này chính là tâm đường tròn ngoại tiếp tam giác.

Ứng dụng của trung trực tam giác

Trung trực của tam giác có nhiều ứng dụng trong hình học, đặc biệt là trong việc dựng hình và giải toán hình học. Ví dụ, nó được sử dụng để tìm tâm đường tròn ngoại tiếp, xác định vị trí của các điểm đặc biệt trong tam giác, và giải các bài toán liên quan đến khoảng cách.

Sản phẩm liên quan: butan + cl2 tỉ lệ 1 1 sản phẩm chính

Sản phẩm liên quan: c6h5oh + fecl3 hiện tượng

Sản phẩm hữu ích: bộ nồi đức 3 món

Xem thêm: thiên sơn suối ngà có gì

Sản phẩm hữu ích: đổi từ mét khối sang lít