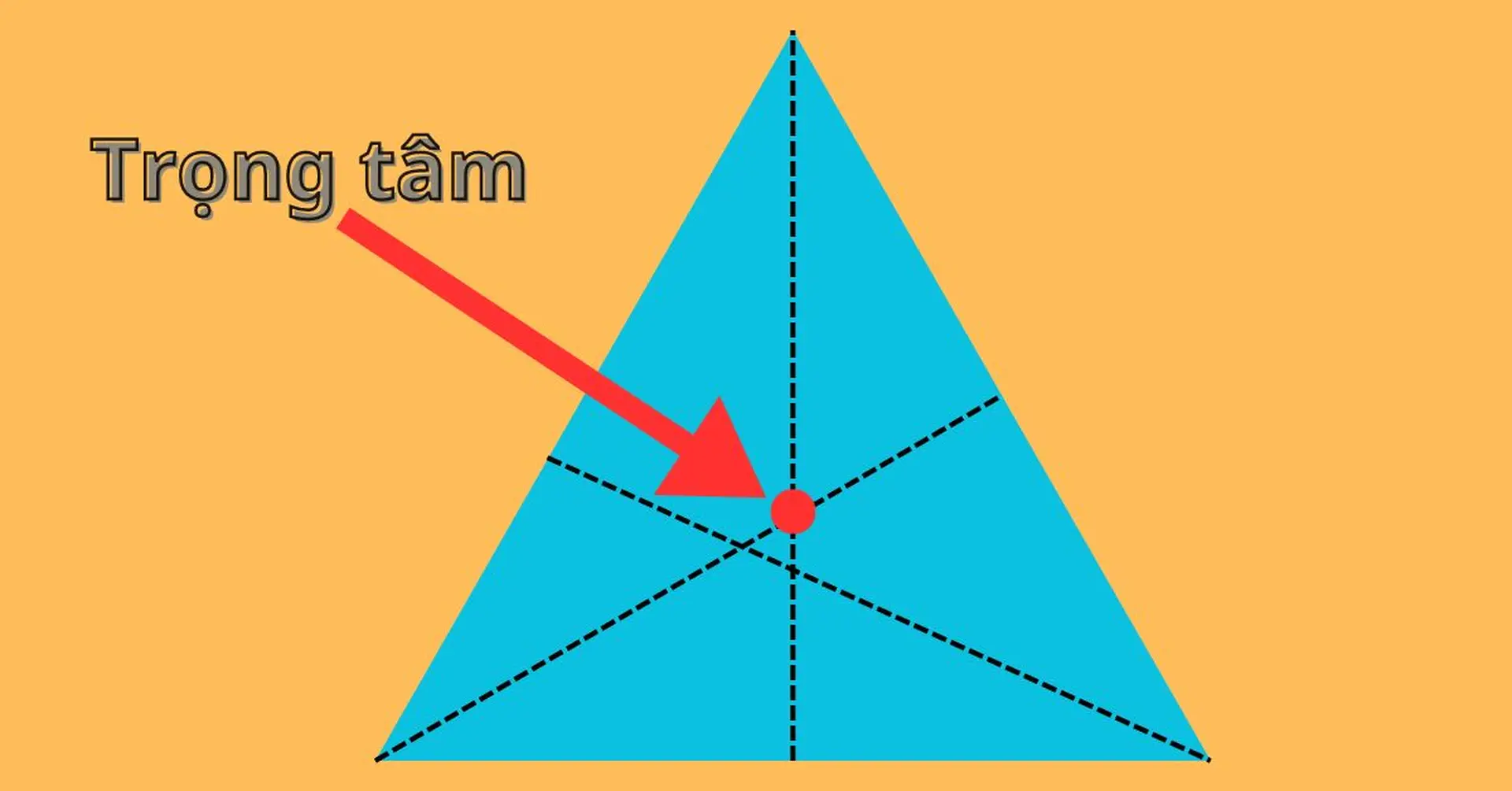
Trọng Tâm Tam Giác Đều Cạnh a

Mô tả sản phẩm

Trọng tâm của tam giác đều cạnh a nằm trên đường trung tuyến, cách mỗi đỉnh một khoảng bằng 2a/3. Nó cũng là giao điểm của ba đường trung tuyến, ba đường trung trực, và ba đường cao của tam giác.

Tìm hiểu về trọng tâm tam giác đều

Định nghĩa trọng tâm

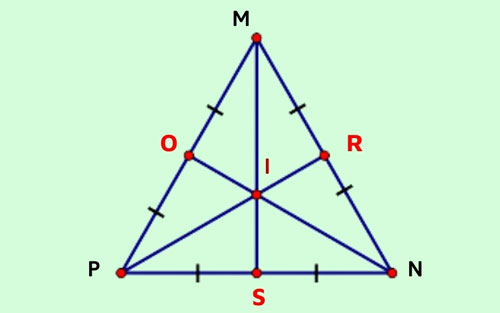
Trọng tâm của một tam giác là giao điểm của ba đường trung tuyến. Đường trung tuyến là đoạn thẳng nối một đỉnh của tam giác với trung điểm của cạnh đối diện. Trong tam giác đều, ba đường trung tuyến đồng thời là ba đường cao, ba đường trung trực và ba phân giác.

Tính toán tọa độ trọng tâm

Giả sử tam giác đều ABC có cạnh a. Đặt A tại gốc tọa độ (0, 0). Nếu đặt B tại (a, 0), thì C sẽ có tọa độ (a/2, a√3/2). Trọng tâm G sẽ có tọa độ là trung bình cộng tọa độ của ba đỉnh: G = ((0+a+a/2)/3, (0+0+a√3/2)/3) = (a/2, a√3/6). Khoảng cách từ trọng tâm đến mỗi đỉnh là 2a/3.

Ứng dụng của trọng tâm tam giác đều

Hiểu về trọng tâm tam giác đều có nhiều ứng dụng trong toán học, vật lý và kỹ thuật. Ví dụ:

• Trong cơ học, trọng tâm là điểm mà ta có thể coi trọng lực tác dụng lên toàn bộ tam giác.
• Trong thiết kế, hiểu về trọng tâm giúp phân bố tải trọng hiệu quả.
• Trong hình học, trọng tâm là một điểm đặc biệt có nhiều tính chất quan trọng.

Công thức tính khoảng cách từ trọng tâm đến đỉnh

Khoảng cách từ trọng tâm G đến mỗi đỉnh của tam giác đều cạnh a luôn bằng 2a/3. Đây là một tính chất đặc trưng của tam giác đều.

Tổng kết

Trọng tâm của tam giác đều cạnh a là một điểm quan trọng với nhiều tính chất đặc biệt. Việc hiểu rõ về vị trí và tính chất của trọng tâm giúp giải quyết nhiều bài toán liên quan đến tam giác đều.

Xem thêm: phát biểu định luật về công

Sản phẩm liên quan: tai thỏ là gì

Xem thêm: khi con lắc đơn dao động đến vị trí cao nhất

Sản phẩm liên quan: thi toán tiếng anh

Sản phẩm liên quan: bacl2 + mgso4 → ?