Trong Tam Giác Vuông Cạnh Huyền Bằng

Mô tả sản phẩm

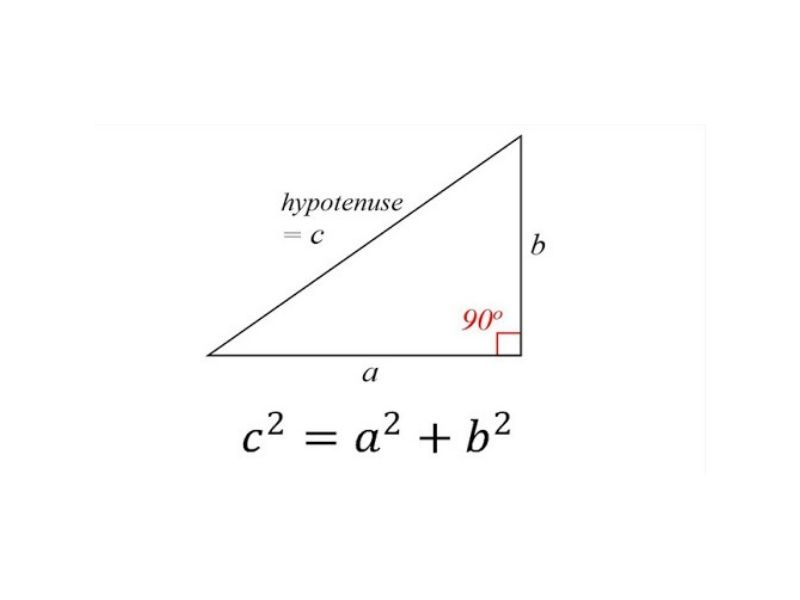
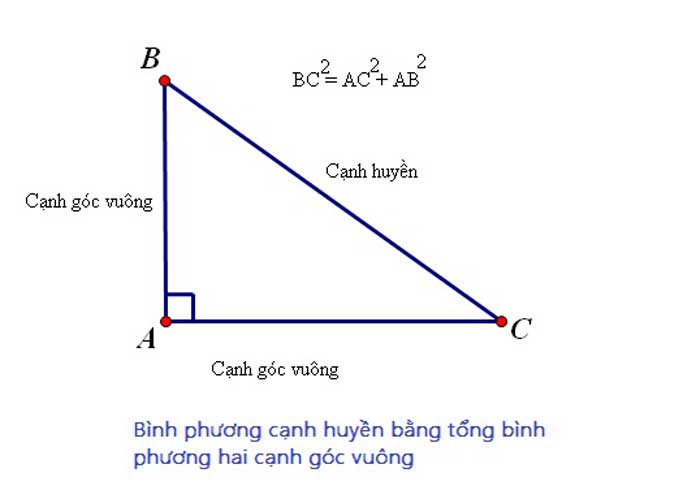
Trong tam giác vuông, cạnh huyền bằng tổng bình phương của hai cạnh góc vuông. Đây là định lý Pitago nổi tiếng. Cụ thể hơn, nếu tam giác vuông ABC có cạnh huyền BC và hai cạnh góc vuông AB và AC, thì BC² = AB² + AC².

Ứng dụng của Định lý Pitago

Tính độ dài cạnh huyền:

Nếu biết độ dài hai cạnh góc vuông, ta có thể tính độ dài cạnh huyền bằng cách áp dụng công thức: Cạnh huyền = √(cạnh góc vuông 1² + cạnh góc vuông 2²). Ví dụ: nếu AB = 3cm và AC = 4cm, thì BC = √(3² + 4²) = √25 = 5cm.

Tính độ dài cạnh góc vuông:

Nếu biết độ dài cạnh huyền và một cạnh góc vuông, ta có thể tính độ dài cạnh góc vuông còn lại. Ví dụ: nếu BC = 5cm và AB = 3cm, thì AC = √(BC² - AB²) = √(5² - 3²) = √16 = 4cm.

Ví dụ minh họa

Ví dụ 1:

Một chiếc thang dài 10m được dựa vào tường, chân thang cách tường 6m. Hỏi thang cao bao nhiêu mét trên tường? Đây là một ví dụ điển hình áp dụng định lý Pitago để tính độ cao của thang trên tường. Độ cao này chính là một cạnh góc vuông, và độ dài thang là cạnh huyền. Ta có: Độ cao = √(10² - 6²) = √64 = 8m.

Ví dụ 2:

Một hình chữ nhật có chiều dài 12cm và đường chéo 13cm. Tính chiều rộng của hình chữ nhật. Đường chéo của hình chữ nhật chính là cạnh huyền của tam giác vuông được tạo bởi chiều dài và chiều rộng. Ta có: Chiều rộng = √(13² - 12²) = √25 = 5cm.

Xem thêm: truyện thể loại trâu già gặm cỏ non

Sản phẩm liên quan: tiếng việt nâng cao lớp 2 có đáp án

Sản phẩm liên quan: bài mồi câu chép tự nhiên

Sản phẩm liên quan: công tắc trong máy lọc nước kangaroo