Trong tam giác đều đường trung tuyến đồng thời là đường gì?

Chính Sách Vận Chuyển Và Đổi Trả Hàng
Miễn phí vận chuyển mọi đơn hàng từ 500K
- Phí ship mặc trong nước 50K
- Thời gian nhận hàng 2-3 ngày trong tuần
- Giao hàng hỏa tốc trong 24h
- Hoàn trả hàng trong 30 ngày nếu không hài lòng
Mô tả sản phẩm
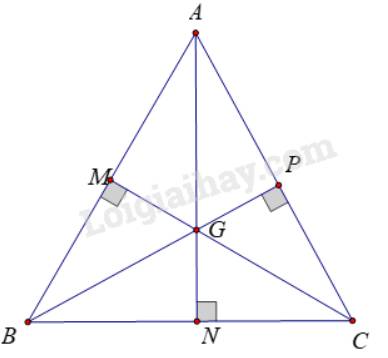
Trong tam giác đều, đường trung tuyến đồng thời là đường cao, đường phân giác và đường trung trực.
Chứng minh đường trung tuyến trong tam giác đều là đường cao
Tính chất tam giác đều
Tam giác đều là tam giác có ba cạnh bằng nhau và ba góc bằng nhau, mỗi góc bằng 60 độ. Do đó, trong tam giác đều, mọi đường trung tuyến đều chia tam giác thành hai tam giác cân.
Chứng minh
Xét tam giác đều ABC, với M là trung điểm của BC. Ta cần chứng minh AM vuông góc với BC. Vì tam giác ABC đều nên AB = AC = BC. Trong tam giác ABM và ACM, ta có: AB = AC, BM = CM (M là trung điểm BC), AM là cạnh chung. Theo trường hợp cạnh - cạnh - cạnh (c.c.c), tam giác ABM = tam giác ACM. Do đó, góc AMB = góc AMC. Mà góc AMB + góc AMC = 180 độ (hai góc kề bù), nên góc AMB = góc AMC = 90 độ. Vậy AM vuông góc với BC, tức là AM là đường cao.
Chứng minh đường trung tuyến trong tam giác đều là đường phân giác và đường trung trực
Đường phân giác
Vì tam giác ABM = tam giác ACM (chứng minh trên), nên góc BAM = góc CAM. Do đó, AM là đường phân giác của góc BAC.
Đường trung trực
Vì AM là đường cao và M là trung điểm BC, nên AM vuông góc với BC tại trung điểm M. Điều này chứng tỏ AM là đường trung trực của BC.
Tóm lại, trong một tam giác đều, đường trung tuyến đóng vai trò quan trọng, nó đồng thời là đường cao, đường phân giác và đường trung trực.
Sản phẩm hữu ích: lời bài hát thơ tình cuối mùa thu
Sản phẩm liên quan: c6h12o6 là chất gì
Sản phẩm hữu ích: búp bê cầu nắng và búp bê cầu mưa
Sản phẩm liên quan: tác dụng của 3b