Trong tam giác đều đường cao bằng bao nhiêu?

Mô tả sản phẩm

Trong tam giác đều, đường cao bằng a√3/2, trong đó a là độ dài cạnh của tam giác.

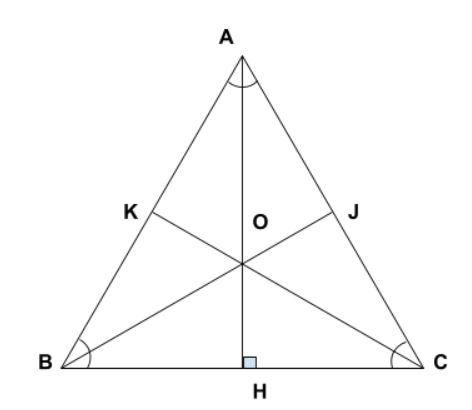
Mối quan hệ giữa cạnh và đường cao trong tam giác đều

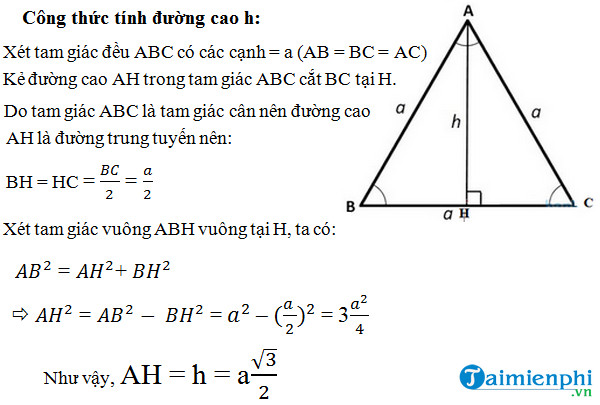
Công thức tính đường cao

Đường cao trong tam giác đều có mối liên hệ chặt chẽ với độ dài cạnh của tam giác. Giả sử cạnh của tam giác đều là a, thì đường cao h được tính theo công thức: h = a√3/2. Công thức này được suy ra từ định lý Pytago, áp dụng vào tam giác vuông tạo bởi đường cao và một nửa cạnh đáy của tam giác đều.

Ví dụ minh họa

Ví dụ: Nếu một tam giác đều có cạnh bằng 6cm, thì đường cao của tam giác đó sẽ là: h = 6√3/2 = 3√3 cm.

Ứng dụng của công thức tính đường cao trong tam giác đều

Tính diện tích tam giác đều

Biết đường cao, ta có thể dễ dàng tính diện tích tam giác đều bằng công thức: S = (1/2) * a * h. Thay h = a√3/2 vào công thức trên, ta được công thức tính diện tích tam giác đều dựa trên cạnh: S = (a²√3)/4.

Giải bài toán hình học

Công thức tính đường cao tam giác đều được ứng dụng rộng rãi trong giải quyết các bài toán hình học phức tạp hơn, liên quan đến tính toán diện tích, thể tích, hay tìm các yếu tố hình học khác trong các hình phức tạp hơn chứa tam giác đều.

Ứng dụng thực tiễn

Trong thực tiễn, công thức này được sử dụng trong nhiều lĩnh vực, từ kiến trúc, xây dựng cho đến thiết kế đồ họa và nhiều lĩnh vực kỹ thuật khác.

Sản phẩm liên quan: đặc điểm biến dạng của lò xo

Sản phẩm hữu ích: sườn xám tiếng anh

Sản phẩm hữu ích: ví dụ về sự ngưng tụ

Sản phẩm liên quan: al(oh)3 asam atau basa