Toán 9 Kỳ 2: Tổng hợp kiến thức và bài tập


Chính Sách Vận Chuyển Và Đổi Trả Hàng
Miễn phí vận chuyển mọi đơn hàng từ 500K
- Phí ship mặc trong nước 50K
- Thời gian nhận hàng 2-3 ngày trong tuần
- Giao hàng hỏa tốc trong 24h
- Hoàn trả hàng trong 30 ngày nếu không hài lòng
Mô tả sản phẩm
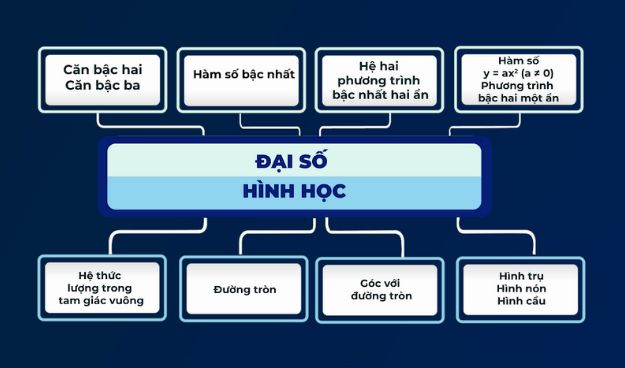
Toán 9 kỳ 2 bao gồm các chương về hàm số bậc hai, phương trình bậc hai, hệ phương trình bậc nhất hai ẩn, đường tròn, và các bài toán liên quan. Nội dung này sẽ giúp bạn nắm vững kiến thức và làm bài tập hiệu quả.
Chương 1: Hàm số bậc hai
Đồ thị hàm số y = ax2 (a ≠ 0)
Chương này giới thiệu về khái niệm hàm số bậc hai, đồ thị của hàm số bậc hai, cách vẽ đồ thị và ứng dụng của đồ thị trong giải các bài toán thực tế. Bạn sẽ học cách xác định đỉnh parabol, trục đối xứng và các điểm đặc biệt trên đồ thị.
Hàm số y = ax2 + bx + c (a ≠ 0)
Phần này mở rộng kiến thức về hàm số bậc hai với dạng tổng quát hơn, bao gồm việc xác định các yếu tố như đỉnh parabol, trục đối xứng, giao điểm với trục Ox và Oy. Bạn sẽ được làm quen với các phương pháp tìm giá trị lớn nhất, nhỏ nhất của hàm số.
Chương 2: Phương trình bậc hai một ẩn
Phương trình bậc hai và cách giải
Chương này trình bày các phương pháp giải phương trình bậc hai một ẩn như công thức nghiệm, phương pháp phân tích đa thức thành nhân tử, phương pháp sử dụng định lý Vi-ét. Bạn sẽ học cách tìm nghiệm, xác định số nghiệm và ứng dụng vào giải bài toán thực tế.
Ứng dụng của phương trình bậc hai
Phần này sẽ hướng dẫn bạn cách áp dụng phương trình bậc hai để giải các bài toán liên quan đến hình học, vật lý và các bài toán thực tế khác. Bạn sẽ được làm quen với các dạng bài tập đa dạng và nâng cao.
Chương 3: Hệ phương trình bậc nhất hai ẩn
Phương pháp giải hệ phương trình
Chương này giới thiệu các phương pháp giải hệ phương trình bậc nhất hai ẩn như phương pháp thế, phương pháp cộng đại số và cách sử dụng máy tính bỏ túi để giải hệ phương trình. Bạn sẽ học cách xác định nghiệm của hệ phương trình và ứng dụng vào giải các bài toán thực tế.
Ứng dụng của hệ phương trình
Phần này tập trung vào việc ứng dụng hệ phương trình để giải quyết các bài toán thực tiễn liên quan đến nhiều đại lượng chưa biết, giúp bạn hiểu rõ hơn về ý nghĩa thực tế của hệ phương trình.
Chương 4: Đường tròn
Khái niệm và tính chất của đường tròn
Chương này sẽ giới thiệu khái niệm đường tròn, các yếu tố của đường tròn như tâm, bán kính, đường kính, dây cung, cung tròn. Bạn sẽ học các tính chất cơ bản của đường tròn và các định lý liên quan.
Phương trình đường tròn
Phần này trình bày phương trình đường tròn và cách xác định tâm và bán kính của đường tròn từ phương trình. Bạn sẽ học cách viết phương trình đường tròn khi biết các yếu tố của nó và ứng dụng vào giải các bài toán.
Sản phẩm liên quan: những bài hát ru con ngủ miền nam
Sản phẩm liên quan: vẽ lọ hoa sen
Sản phẩm liên quan: f cl br i
Xem thêm: xê xích là gì