Toán 9 Bài 4 Hình Học Chương 2: Hệ Thức Lượng Trong Tam Giác Vuông

Mô tả sản phẩm

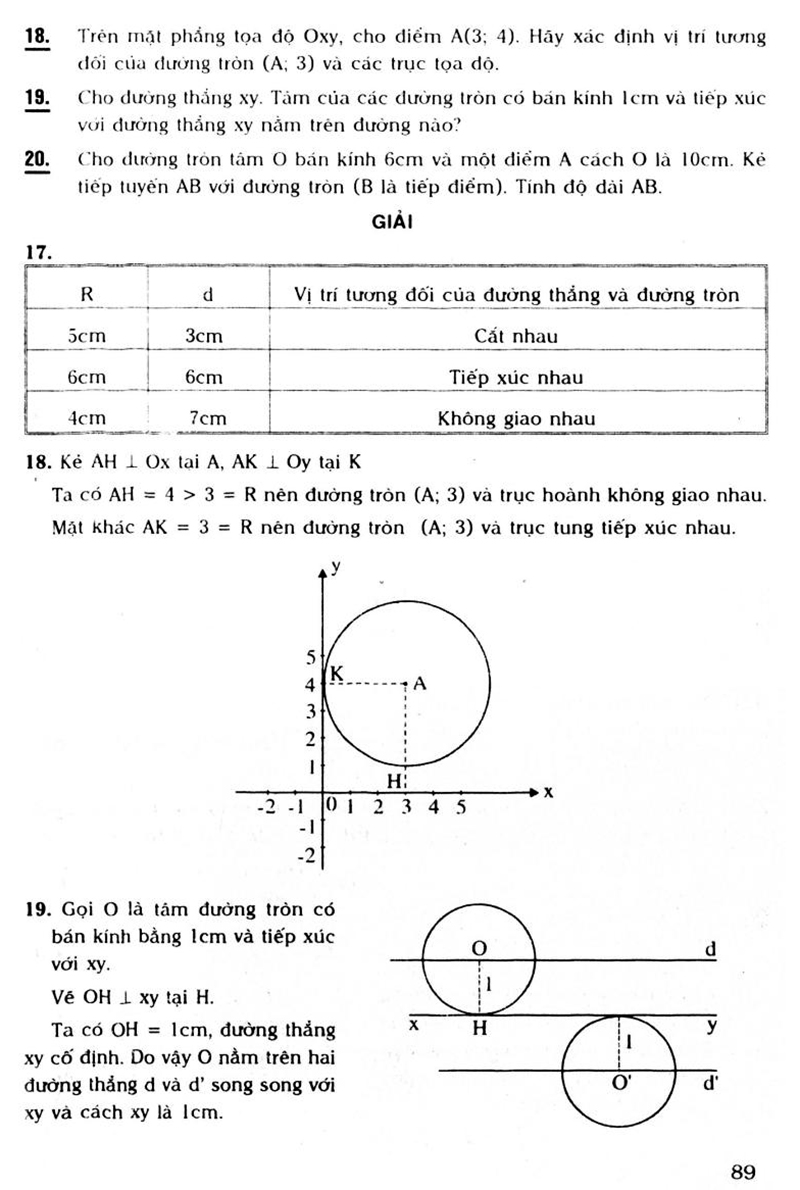
Toán 9 bài 4 hình học chương 2 chủ yếu xoay quanh hệ thức lượng trong tam giác vuông. Bài học này giúp bạn hiểu và áp dụng các công thức để tính toán các cạnh, chiều cao và các yếu tố khác trong tam giác vuông. Bạn sẽ học cách sử dụng định lý Pytago, các hệ thức về cạnh và đường cao trong tam giác vuông để giải quyết các bài toán thực tế.

Định Lý Pytago và Hệ Quả

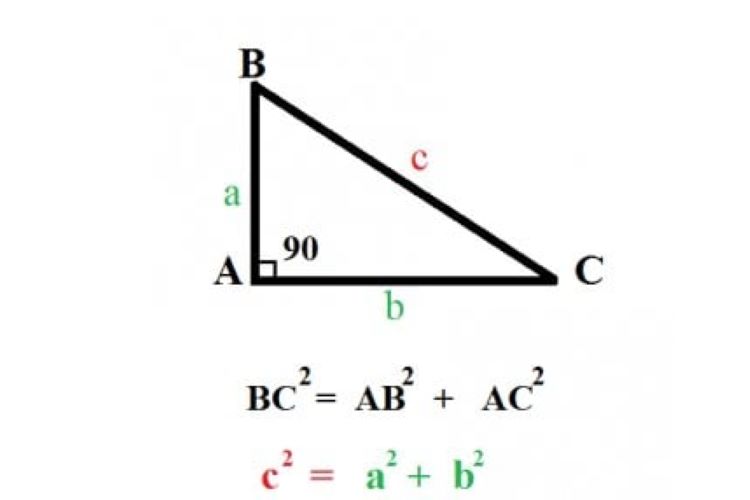
Định lý Pytago:

Trong một tam giác vuông, bình phương của cạnh huyền bằng tổng các bình phương của hai cạnh góc vuông. Công thức: a² = b² + c² (với a là cạnh huyền, b và c là hai cạnh góc vuông). Bài học sẽ hướng dẫn bạn cách áp dụng định lý này để tính độ dài các cạnh trong tam giác vuông.

Hệ quả của định lý Pytago:

Từ định lý Pytago, ta suy ra được các hệ quả quan trọng giúp giải quyết nhiều bài toán phức tạp hơn. Ví dụ, nếu biết độ dài hai cạnh của tam giác vuông, ta có thể tính được độ dài cạnh còn lại.

Hệ Thức Lượng Trong Tam Giác Vuông

Hệ thức giữa cạnh và đường cao:

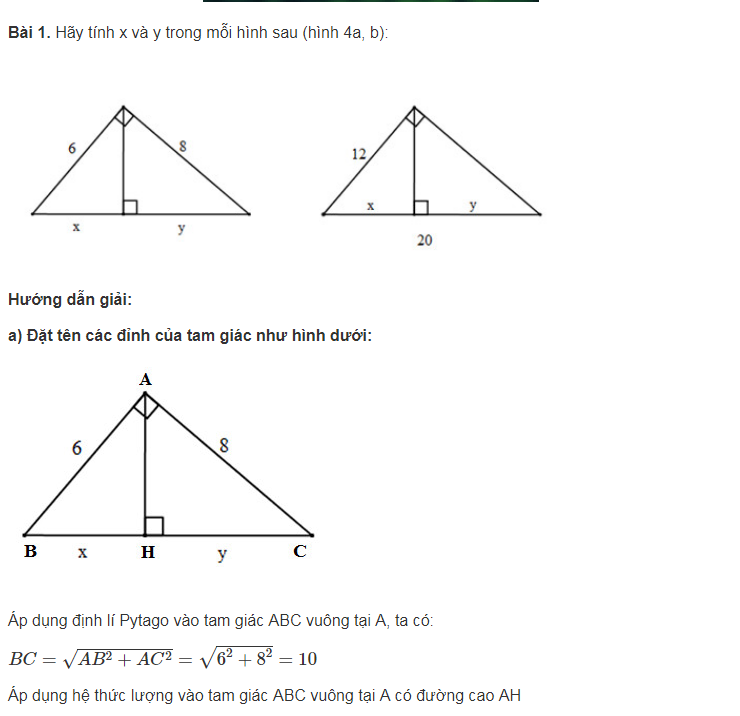
Bài học sẽ trình bày các hệ thức liên hệ giữa độ dài các cạnh và đường cao trong tam giác vuông. Bạn sẽ học cách sử dụng các công thức này để tính độ dài đường cao, độ dài các cạnh khi biết một số thông tin khác. Ví dụ: h² = b'c' (với h là đường cao ứng với cạnh huyền, b' và c' là hai đoạn thẳng mà đường cao chia cạnh huyền thành).

Hệ thức giữa cạnh huyền và hình chiếu của các cạnh góc vuông trên cạnh huyền:

Bài học sẽ giới thiệu các công thức liên hệ giữa cạnh huyền và hình chiếu của các cạnh góc vuông lên cạnh huyền. Việc nắm vững các công thức này rất quan trọng để giải quyết các bài toán về tính toán độ dài trong tam giác vuông. Ví dụ: b² = a.b'; c² = a.c'

Bài Tập Áp Dụng

Bài học sẽ cung cấp nhiều ví dụ minh họa và bài tập áp dụng giúp bạn củng cố kiến thức và kỹ năng giải toán. Việc làm nhiều bài tập là rất cần thiết để bạn thành thạo các công thức và ứng dụng chúng một cách linh hoạt. Bạn nên tự mình giải quyết các bài tập trước khi xem đáp án để đạt được hiệu quả học tập tốt nhất. Lưu ý phân loại các dạng bài tập để có phương pháp giải phù hợp.

Sản phẩm liên quan: nổi hột dưới lưỡi

Sản phẩm hữu ích: bút toán xóa sổ tài sản cố định

Xem thêm: nước muối có tác dụng gì