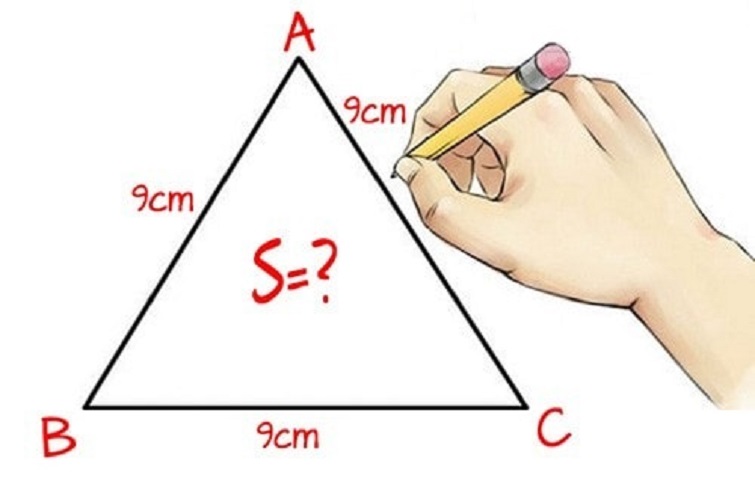
Tính diện tích tam giác khi biết 3 cạnh

Mô tả sản phẩm

Để tính diện tích tam giác khi biết độ dài ba cạnh a, b, c, ta sử dụng công thức Heron. Công thức này cho phép tính diện tích tam giác mà không cần biết góc nào của tam giác.

Công thức Heron

Công thức tính nửa chu vi

Trước tiên, ta cần tính nửa chu vi (p) của tam giác:
p = (a + b + c) / 2
trong đó:
* a, b, c là độ dài ba cạnh của tam giác.

Công thức tính diện tích

Sau khi tính được nửa chu vi, ta áp dụng công thức Heron để tính diện tích (S) của tam giác:
S = √[p(p - a)(p - b)(p - c)]
trong đó:
* p là nửa chu vi của tam giác. * a, b, c là độ dài ba cạnh của tam giác.

Ví dụ minh họa

Giả sử ta có một tam giác với ba cạnh có độ dài lần lượt là a = 5cm, b = 6cm, c = 7cm. Ta thực hiện các bước tính toán như sau:
1. Tính nửa chu vi: p = (5 + 6 + 7) / 2 = 9 cm
2. Áp dụng công thức Heron: S = √[9(9 - 5)(9 - 6)(9 - 7)] = √[9 * 4 * 3 * 2] = √216 ≈ 14.7 cm²
Vậy diện tích của tam giác này xấp xỉ 14.7 cm².

Ứng dụng của công thức Heron

Công thức Heron được ứng dụng rộng rãi trong nhiều lĩnh vực, bao gồm:
* Tính toán diện tích đất đai trong đo đạc.
* Giải quyết các bài toán hình học phức tạp.
* Sử dụng trong các phần mềm thiết kế và lập trình.

Lưu ý

Để công thức Heron có nghĩa, điều kiện cần là độ dài ba cạnh phải thỏa mãn bất đẳng thức tam giác: tổng độ dài hai cạnh bất kỳ phải lớn hơn độ dài cạnh còn lại. Nếu điều kiện này không được thỏa mãn, thì không tồn tại tam giác với ba cạnh đó.

Sản phẩm hữu ích: đặc điểm của nam châm

Sản phẩm liên quan: vẽ bức tranh về gia đình

Xem thêm: file nghe family and friends 3

Sản phẩm hữu ích: nhận xét học bạ môn tin học lớp 3

Xem thêm: đề thi khảo sát toán 9