Tính nhanh đạo hàm bậc 2 trên bậc 2
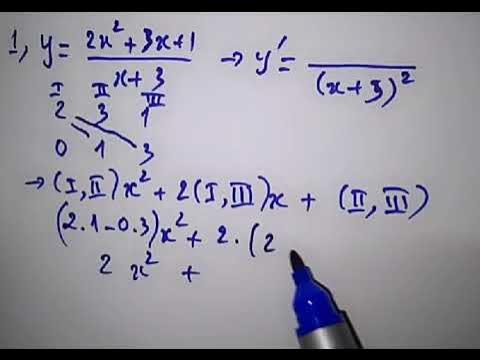


Chính Sách Vận Chuyển Và Đổi Trả Hàng
Miễn phí vận chuyển mọi đơn hàng từ 500K
- Phí ship mặc trong nước 50K
- Thời gian nhận hàng 2-3 ngày trong tuần
- Giao hàng hỏa tốc trong 24h
- Hoàn trả hàng trong 30 ngày nếu không hài lòng
Mô tả sản phẩm
Tính nhanh đạo hàm bậc 2 của hàm số bậc 2 là một kỹ thuật quan trọng trong giải tích. Phương pháp này giúp tiết kiệm thời gian và công sức so với việc tính toán trực tiếp bằng định nghĩa. Nói tóm lại, đạo hàm bậc hai của một hàm số bậc hai luôn là một hằng số.
Công thức tính nhanh đạo hàm bậc 2 của hàm số bậc 2
Hàm số bậc hai tổng quát
Giả sử ta có hàm số bậc hai tổng quát: f(x) = ax² + bx + c, với a, b, c là các hằng số và a ≠ 0. Đạo hàm bậc nhất là f'(x) = 2ax + b. Đạo hàm bậc hai, f''(x), là đạo hàm của đạo hàm bậc nhất, và trong trường hợp này, f''(x) = 2a. Như vậy, đạo hàm bậc hai của một hàm số bậc hai luôn là một hằng số bằng hai lần hệ số của x².Ví dụ minh họa
Cho hàm số f(x) = 3x² + 5x - 2. Theo công thức trên, đạo hàm bậc hai của f(x) là f''(x) = 2 * 3 = 6. Chúng ta không cần phải tính đạo hàm bậc nhất rồi lại tính đạo hàm của đạo hàm bậc nhất. Kết quả luôn là gấp đôi hệ số của x².Ứng dụng của việc tính nhanh đạo hàm bậc 2
Việc tính nhanh đạo hàm bậc hai của hàm số bậc hai có ứng dụng rộng rãi trong nhiều lĩnh vực, đặc biệt là:Vật lý
Trong cơ học, đạo hàm bậc hai của vị trí theo thời gian cho gia tốc. Nếu vị trí được mô tả bởi một hàm số bậc hai, việc tính gia tốc trở nên đơn giản hơn rất nhiều.Kỹ thuật
Trong kỹ thuật, đạo hàm bậc hai được sử dụng để xác định độ cong của đường cong, rất hữu ích trong thiết kế đường cong và phân tích cấu trúc.Thống kê
Trong thống kê, đạo hàm bậc hai được dùng trong việc tìm cực trị của hàm likelihood, giúp xác định các tham số của mô hình.Sản phẩm liên quan: c3h8o o2 co2 h2o
Sản phẩm hữu ích: mùi gì đuổi chó
Sản phẩm liên quan: pin mặt trời biến đổi năng lượng ánh sáng thành dạng năng lượng nào
Xem thêm: c2h5oh có tác dụng với br2 không