Tính Giới Hạn của Hàm Số


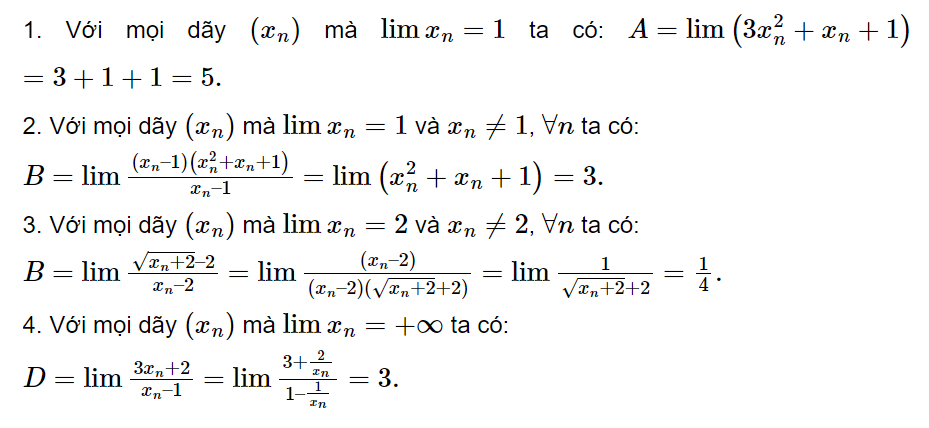
Chính Sách Vận Chuyển Và Đổi Trả Hàng
Miễn phí vận chuyển mọi đơn hàng từ 500K
- Phí ship mặc trong nước 50K
- Thời gian nhận hàng 2-3 ngày trong tuần
- Giao hàng hỏa tốc trong 24h
- Hoàn trả hàng trong 30 ngày nếu không hài lòng
Mô tả sản phẩm
Giới hạn của hàm số là một khái niệm quan trọng trong giải tích, giúp chúng ta hiểu hành vi của hàm số khi biến số tiến tới một giá trị cụ thể hoặc vô cực. Nó cho biết giá trị mà hàm số "tiến gần" khi biến số x tiến gần tới một điểm nào đó. Hiểu rõ giới hạn của hàm số là nền tảng để nghiên cứu đạo hàm, tích phân và nhiều khái niệm toán học cao cấp khác.
Khái niệm Giới Hạn
Giới hạn hữu hạn:
Khi x tiến tới a, hàm số f(x) tiến tới một giá trị L hữu hạn, ta viết: limx→a f(x) = L. Điều này có nghĩa là ta có thể làm cho giá trị của f(x) "cận kề" L bao nhiêu cũng được bằng cách chọn x đủ gần a (nhưng khác a).Giới hạn vô cực:
Khi x tiến tới a, hàm số f(x) có giá trị tuyệt đối tiến tới vô cực, ta viết: limx→a f(x) = ∞ hoặc limx→a f(x) = -∞. Điều này có nghĩa là giá trị của f(x) trở nên rất lớn (hoặc rất nhỏ) khi x tiến gần tới a.Giới hạn khi x tiến tới vô cực:
Khi x tiến tới vô cực dương (x → ∞) hoặc vô cực âm (x → -∞), hàm số f(x) tiến tới một giá trị L, ta viết: limx→∞ f(x) = L hoặc limx→-∞ f(x) = L. Điều này mô tả hành vi của hàm số khi x trở nên rất lớn (hoặc rất nhỏ).Các Định lý về Giới Hạn
Có nhiều định lý quan trọng giúp tính toán giới hạn của hàm số một cách dễ dàng hơn, ví dụ như: giới hạn của tổng, hiệu, tích, thương của các hàm số; giới hạn của hàm hợp; quy tắc L'Hôpital (đối với trường hợp 0/0 hoặc ∞/∞). Việc hiểu và áp dụng thành thạo các định lý này là rất cần thiết để giải quyết các bài toán liên quan đến giới hạn.Ứng dụng của Giới Hạn
Giới hạn của hàm số có ứng dụng rộng rãi trong nhiều lĩnh vực, bao gồm:- Tính đạo hàm: Đạo hàm của một hàm số tại một điểm được định nghĩa thông qua giới hạn của thương số vi phân.
- Tính tích phân: Tích phân xác định được tính toán bằng giới hạn của tổng Riemann.
- Xác định tiệm cận: Giới hạn giúp xác định các đường tiệm cận đứng, ngang và xiên của đồ thị hàm số.
- Phân tích hành vi của hàm số: Giới hạn cho phép ta hiểu rõ hơn về hành vi của hàm số khi biến số tiến tới các giá trị đặc biệt.
Sản phẩm liên quan: trường hợp cạnh huyền cạnh góc vuông
Xem thêm: dâu tây tiếng anh
Xem thêm: minh hóa là ở đâu
Sản phẩm hữu ích: không khí có thành phần chính là gì
Xem thêm: sắt hộp vuông nhỏ nhất