Tính Đồng Biến Nghịch Biến của Hàm Số Lượng Giác

Mô tả sản phẩm

Bạn đang tìm hiểu về tính đồng biến và nghịch biến của các hàm số lượng giác? Bài viết này sẽ giúp bạn hiểu rõ về vấn đề này thông qua việc phân tích từng hàm số cụ thể. Tóm lại, tính đồng biến nghịch biến của hàm số lượng giác phụ thuộc vào khoảng xác định đang xét và chu kỳ của hàm số.

Hàm số y = sinx

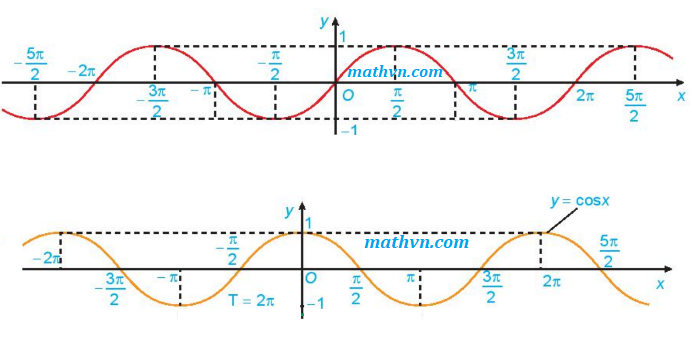
Tính đồng biến và nghịch biến của hàm y = sinx

Hàm số y = sinx đồng biến trên các khoảng (2kπ - π/2; 2kπ + π/2) và nghịch biến trên các khoảng (2kπ + π/2; 2kπ + 3π/2), với k là số nguyên. Điều này có nghĩa là trên mỗi chu kỳ 2π, hàm số sẽ đồng biến trong một nửa chu kỳ và nghịch biến trong nửa chu kỳ còn lại.

Hàm số y = cosx

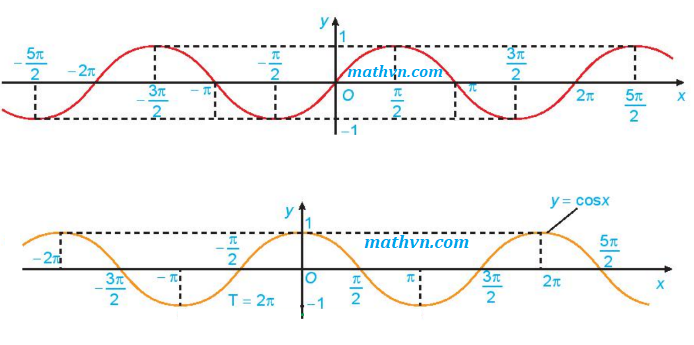
Tính đồng biến và nghịch biến của hàm y = cosx

Hàm số y = cosx nghịch biến trên các khoảng (2kπ; 2kπ + π) và đồng biến trên các khoảng (2kπ - π; 2kπ), với k là số nguyên. Tương tự như hàm sinx, hàm cosx cũng có tính chất đồng biến và nghịch biến xen kẽ nhau trên mỗi chu kỳ 2π.

Hàm số y = tanx

Tính đồng biến và nghịch biến của hàm y = tanx

Hàm số y = tanx đồng biến trên mỗi khoảng (kπ - π/2; kπ + π/2), với k là số nguyên. Lưu ý rằng hàm tanx không xác định tại các điểm x = kπ + π/2.

Hàm số y = cotx

Tính đồng biến và nghịch biến của hàm y = cotx

Hàm số y = cotx nghịch biến trên mỗi khoảng (kπ; kπ + π), với k là số nguyên. Tương tự hàm tanx, hàm cotx không xác định tại các điểm x = kπ. Việc xác định tính đồng biến và nghịch biến của các hàm lượng giác khác phức tạp hơn, thường liên quan đến việc khảo sát đạo hàm của hàm số. Tuy nhiên, việc hiểu rõ tính đồng biến và nghịch biến của các hàm số cơ bản trên sẽ giúp bạn dễ dàng hơn trong việc hiểu và giải quyết các bài toán liên quan.

Sản phẩm liên quan: lớp e là gì

Sản phẩm hữu ích: tán xạ là gì

Xem thêm: hiệu suất là gì