Tính Độ Dài Của Vecto
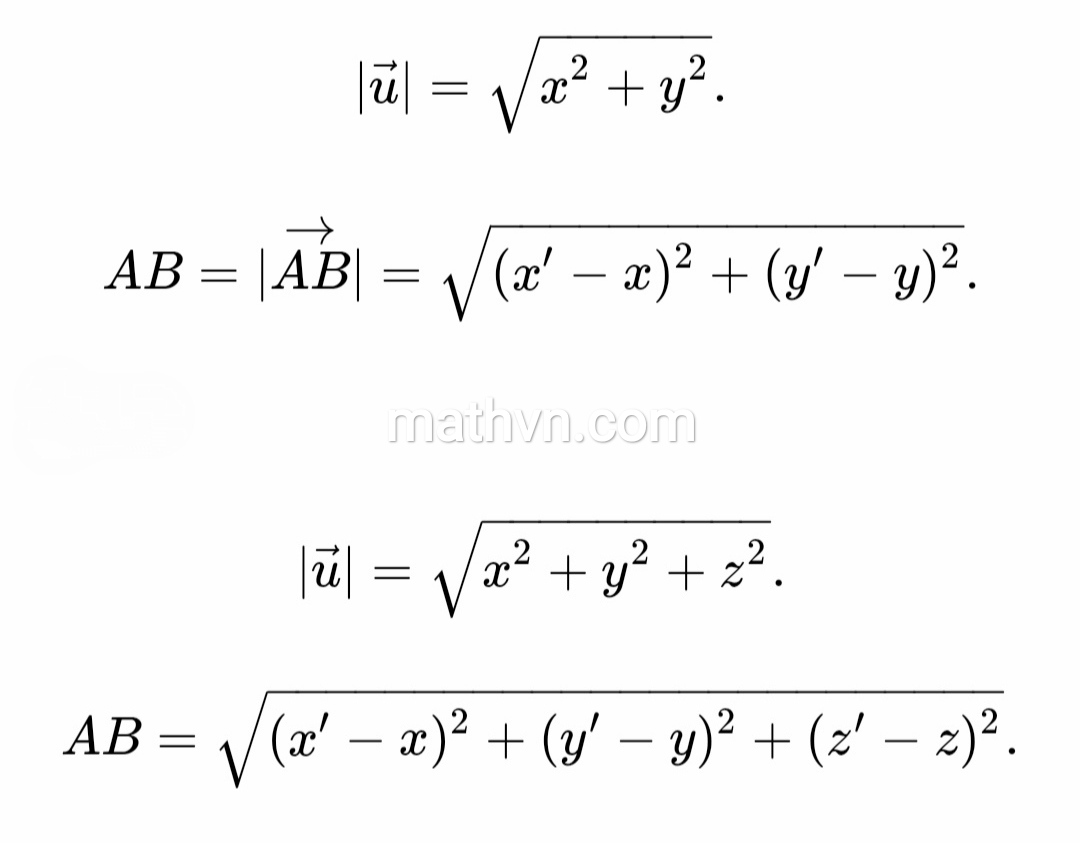
Chính Sách Vận Chuyển Và Đổi Trả Hàng
Miễn phí vận chuyển mọi đơn hàng từ 500K
- Phí ship mặc trong nước 50K
- Thời gian nhận hàng 2-3 ngày trong tuần
- Giao hàng hỏa tốc trong 24h
- Hoàn trả hàng trong 30 ngày nếu không hài lòng
Mô tả sản phẩm
Độ dài của một vecto là khoảng cách từ gốc tọa độ đến điểm cuối của vecto đó. Đối với vecto $\vec{v} = (x, y)$ trong không gian hai chiều, độ dài được tính bằng công thức: $||\vec{v}|| = \sqrt{x^2 + y^2}$. Đối với vecto trong không gian ba chiều hay không gian n chiều, công thức tương tự được áp dụng.
Cách Tính Độ Dài Vecto trong Không Gian Khác Nhau
Không gian hai chiều (R2)
Trong không gian hai chiều, nếu vecto được biểu diễn bởi tọa độ $\vec{v} = (x, y)$, độ dài của vecto được tính theo công thức: $||\vec{v}|| = \sqrt{x^2 + y^2}$. Đây là ứng dụng của định lý Pytago.
Không gian ba chiều (R3)
Trong không gian ba chiều, nếu vecto được biểu diễn bởi tọa độ $\vec{v} = (x, y, z)$, độ dài của vecto được tính theo công thức: $||\vec{v}|| = \sqrt{x^2 + y^2 + z^2}$
Không gian n chiều (Rn)
Tổng quát hóa lên không gian n chiều, nếu vecto được biểu diễn bởi tọa độ $\vec{v} = (x_1, x_2, ..., x_n)$, độ dài của vecto được tính theo công thức: $||\vec{v}|| = \sqrt{x_1^2 + x_2^2 + ... + x_n^2}$. Đây là chuẩn Euclide của vecto.
Ví dụ
Cho vecto $\vec{v} = (3, 4)$. Độ dài của vecto này là: $||\vec{v}|| = \sqrt{3^2 + 4^2} = \sqrt{9 + 16} = \sqrt{25} = 5$
Cho vecto $\vec{u} = (1, 2, 2)$. Độ dài của vecto này là: $||\vec{u}|| = \sqrt{1^2 + 2^2 + 2^2} = \sqrt{1 + 4 + 4} = \sqrt{9} = 3$
Hiểu rõ cách tính độ dài vecto là rất quan trọng trong nhiều lĩnh vực toán học và vật lý, đặc biệt là trong hình học giải tích và cơ học.
Sản phẩm liên quan: ba cô đội gạo lên chùa
Xem thêm: dấu chấm và dấu cộng trong quy tắc bàn tay trái
Sản phẩm liên quan: phát biểu nội dung định luật phản xạ ánh sáng
Sản phẩm hữu ích: vẽ tranh gấu dâu