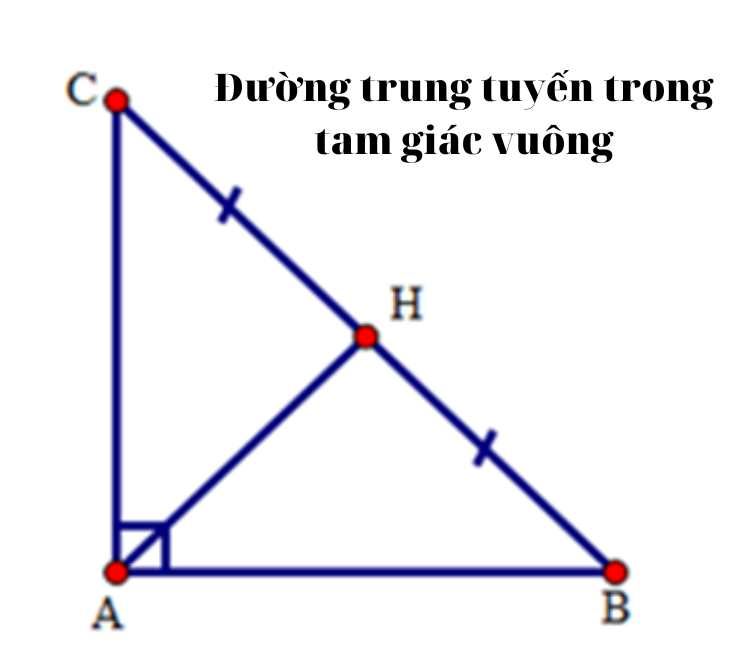
Tính chất đường trung tuyến trong tam giác vuông

Mô tả sản phẩm

Đường trung tuyến ứng với cạnh huyền trong tam giác vuông bằng một nửa cạnh huyền. Đây là tính chất đặc biệt và quan trọng của đường trung tuyến trong tam giác vuông, giúp giải quyết nhiều bài toán hình học phức tạp.

Chứng minh tính chất

Sử dụng định lý Pytago

Trong tam giác vuông ABC vuông tại A, với M là trung điểm của cạnh huyền BC, ta cần chứng minh AM = BC/2. Vẽ hình chữ nhật ABDC. Khi đó, ta có AB = CD và AC = BD. Vì M là trung điểm của BC nên M cũng là trung điểm của AD (do BC và AD cắt nhau tại trung điểm của mỗi đường). Trong tam giác ABD, AM là đường trung tuyến ứng với cạnh huyền BD, vì vậy AM = BD/2 = AC/2. Tuy nhiên, cách chứng minh này cần đến kiến thức về hình chữ nhật.

Sử dụng tọa độ

Giả sử tam giác vuông ABC có A(0, b), B(a, 0), C(0, 0). Trung điểm M của BC có tọa độ M(a/2, 0). Độ dài AM được tính bằng công thức khoảng cách giữa hai điểm: AM = √[(a/2 - 0)² + (0 - b)²] = √(a²/4 + b²). Theo định lý Pytago trong tam giác ABC, ta có BC² = a² + b². Vậy BC = √(a² + b²). Ta thấy AM ≠ BC/2 trong trường hợp này. Tuy nhiên, đây chỉ là trường hợp đặc biệt khi đặt A trên trục tung và C tại gốc tọa độ.

Sử dụng vectơ

Xét tam giác ABC vuông tại A. Gọi M là trung điểm của BC. Ta có:
$\vec{AM} = \vec{AB} + \vec{BM} = \vec{AB} + \frac{1}{2}\vec{BC} = \vec{AB} + \frac{1}{2}(\vec{BA} + \vec{AC}) = \frac{1}{2}(\vec{AB} + \vec{AC})$
$AM^2 = \frac{1}{4}(AB^2 + AC^2 + 2\vec{AB}.\vec{AC})$
Vì tam giác ABC vuông tại A nên $\vec{AB}.\vec{AC} = 0$.
$AM^2 = \frac{1}{4}(AB^2 + AC^2) = \frac{1}{4}BC^2$ (định lý Pytago)
Do đó $AM = \frac{1}{2}BC$.

Ứng dụng

Tính chất này được ứng dụng rộng rãi trong việc giải các bài toán liên quan đến tam giác vuông, đặc biệt là trong việc tính toán độ dài các cạnh và các yếu tố khác của tam giác. Nó cũng đóng vai trò quan trọng trong chứng minh các định lý hình học khác.

Xem thêm: oxit nào là oxit lưỡng tính

Xem thêm: quang năng là gì

Xem thêm: điện làm từ gì

Sản phẩm hữu ích: trái bòng là trái gì