Tính chất đường cao tam giác đều

Mô tả sản phẩm

Đường cao trong tam giác đều có nhiều tính chất đặc biệt. Đó là đường cao đồng thời là đường trung tuyến, đường trung trực và đường phân giác của tam giác. Cụ thể:

Tính chất quan trọng của đường cao tam giác đều

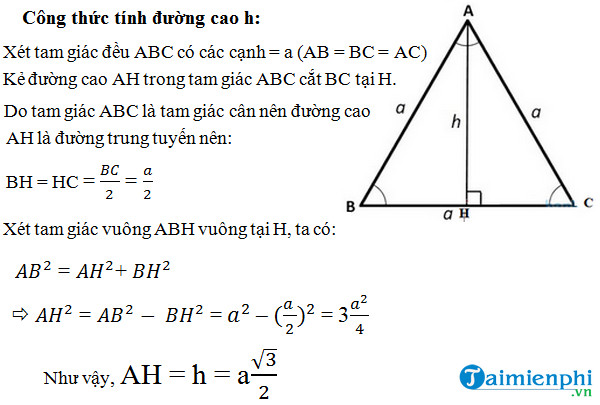
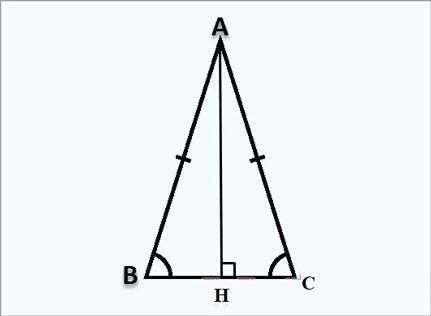
Đường cao là đường trung tuyến:

Đường cao của tam giác đều chia cạnh đáy thành hai đoạn bằng nhau. Điều này có nghĩa là chân đường cao nằm chính giữa cạnh đáy.

Đường cao là đường trung trực:

Đường cao của tam giác đều vuông góc với cạnh đáy tại trung điểm của cạnh đó. Nó cũng chia tam giác đều thành hai tam giác vuông cân.

Đường cao là đường phân giác:

Đường cao của tam giác đều chia góc ở đỉnh thành hai góc bằng nhau, mỗi góc bằng 30 độ.

Độ dài đường cao:

Nếu cạnh của tam giác đều là a, thì độ dài đường cao h được tính bằng công thức: h = a√3/2. Công thức này rất hữu ích trong việc tính toán diện tích và các yếu tố khác của tam giác đều.

Ứng dụng:

Hiểu rõ tính chất đường cao tam giác đều giúp giải quyết nhiều bài toán hình học phức tạp liên quan đến tam giác đều, đặc biệt trong việc tính toán diện tích, chu vi, các góc và các yếu tố khác. Ví dụ, ta có thể sử dụng tính chất này để tính diện tích tam giác đều một cách dễ dàng bằng công thức: S = (a²√3)/4, trong đó a là độ dài cạnh tam giác.

Sản phẩm liên quan: định nghĩa hình tam giác

Xem thêm: bài viết chính tả lớp 2 tập 1

Sản phẩm liên quan: tiếng anh 2 smart start

Sản phẩm hữu ích: bài test tính toán nhanh

Sản phẩm liên quan: hình ảnh con hươu cao cổ