Tính chất của trọng tâm tam giác

Mô tả sản phẩm

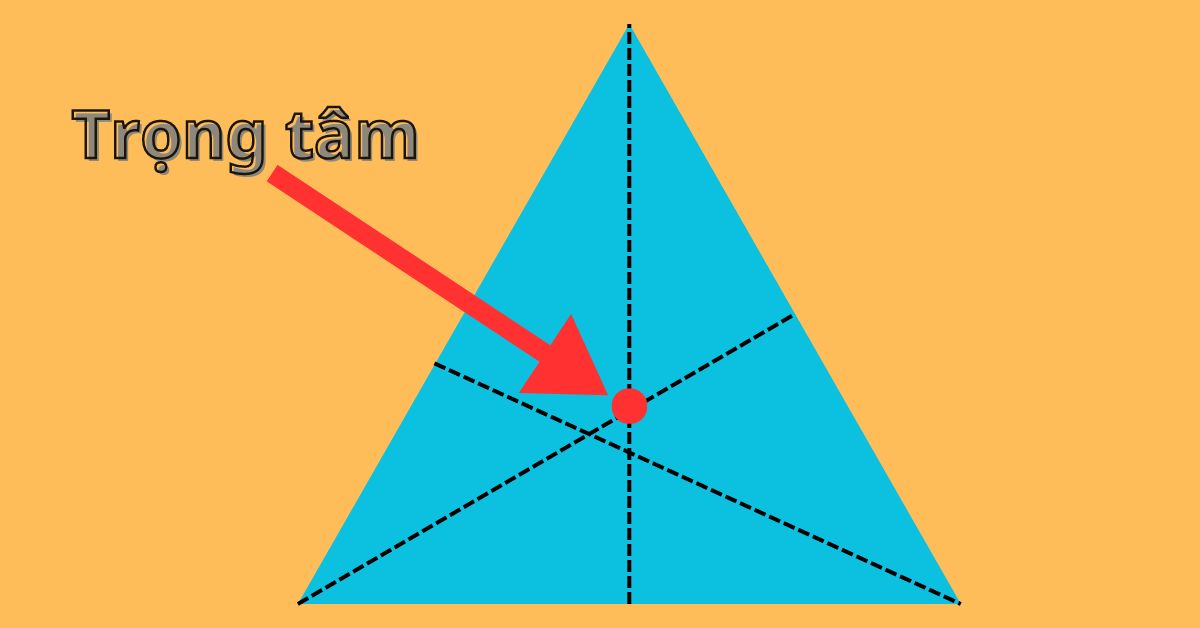
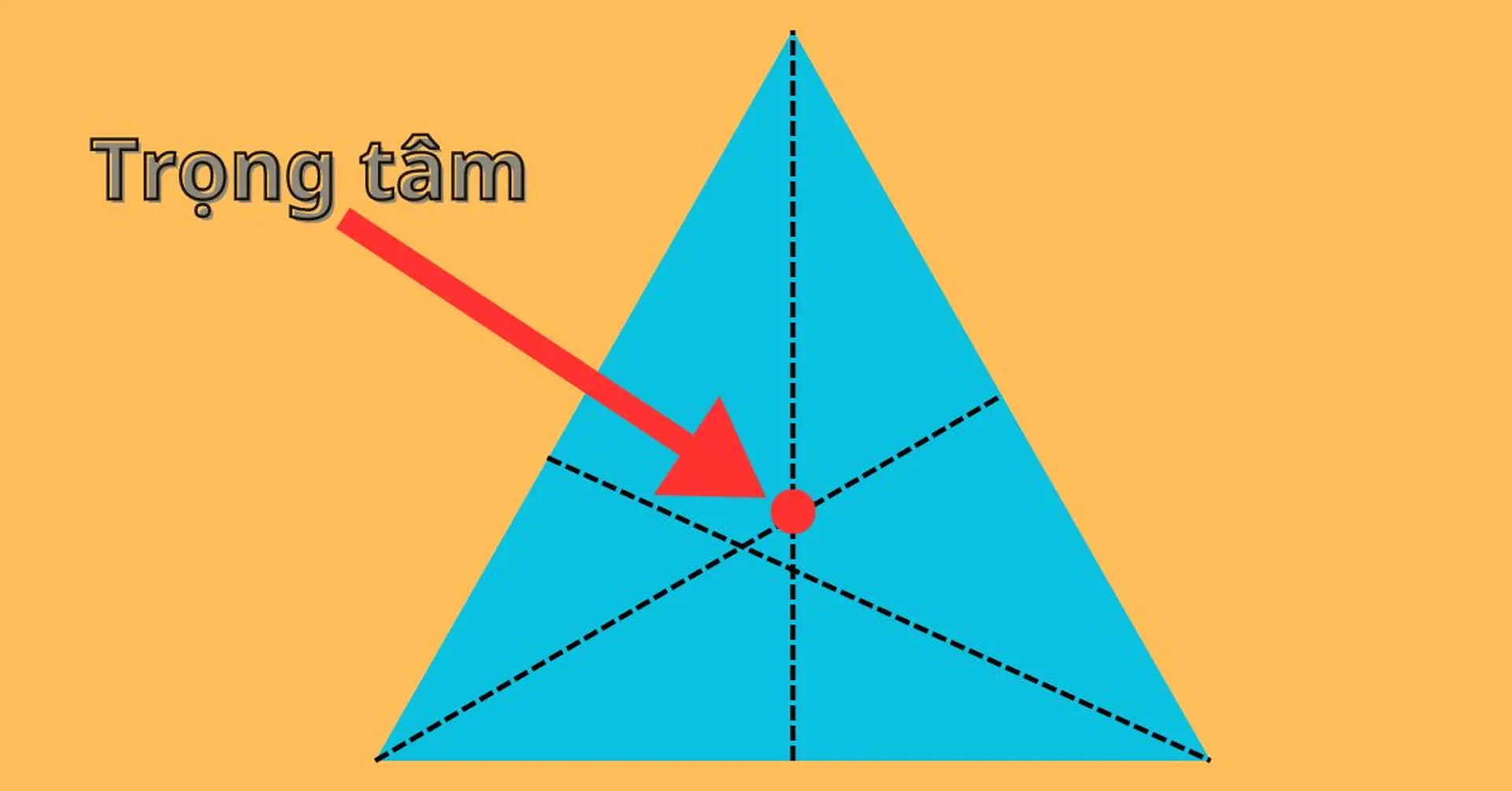
Trọng tâm tam giác là giao điểm của ba đường trung tuyến. Nó có nhiều tính chất quan trọng, bao gồm vị trí chia trung tuyến thành hai đoạn theo tỉ lệ 2:1 và mối liên hệ với tọa độ đỉnh tam giác.

Vị trí của trọng tâm

Tỉ lệ chia trung tuyến:

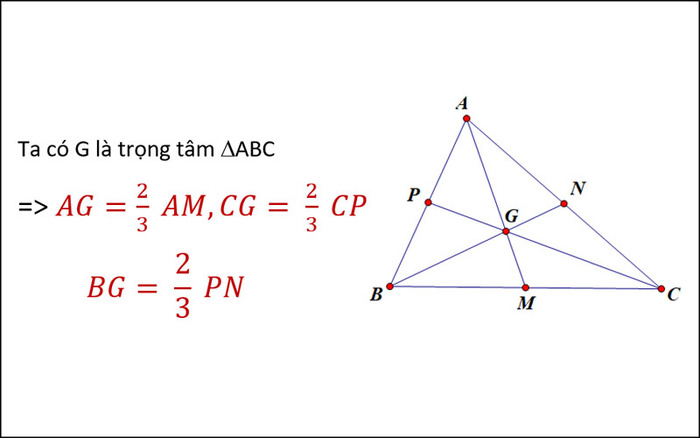
Trọng tâm G chia mỗi đường trung tuyến thành hai đoạn thẳng, trong đó đoạn thẳng từ đỉnh đến trọng tâm dài gấp đôi đoạn thẳng từ trọng tâm đến trung điểm cạnh đối diện. Tức là, nếu M là trung điểm của BC và G là trọng tâm tam giác ABC thì AG = 2GM. Tính chất này rất hữu ích trong việc xác định vị trí trọng tâm khi biết tọa độ các đỉnh của tam giác.

Tọa độ trọng tâm:

Nếu A(x_A, y_A), B(x_B, y_B), C(x_C, y_C) là tọa độ của ba đỉnh tam giác ABC, thì tọa độ trọng tâm G được tính theo công thức: G( (x_A + x_B + x_C)/3, (y_A + y_B + y_C)/3 ). Công thức này cho phép ta dễ dàng xác định vị trí của trọng tâm trên mặt phẳng tọa độ.

Các tính chất khác của trọng tâm

Vectơ:

Trọng tâm G của tam giác ABC có thể biểu diễn bằng vectơ như sau: (Giả sử hình ảnh công thức vectơ được lưu ở file vector_formula.png) Công thức vectơ này cho phép ta áp dụng các phép tính vectơ để giải quyết các bài toán liên quan đến trọng tâm.

Tính chất hình học:

Trọng tâm là điểm đồng quy của ba đường trung tuyến, đồng thời nó cũng là tâm tỉ cự của hệ điểm {A, B, C} với hệ số tỉ lệ {1, 1, 1}. Trọng tâm nằm bên trong tam giác. Nó là tâm đối xứng của tam giác khi và chỉ khi tam giác đó là tam giác đều.

Sản phẩm liên quan: keo 502 bao nhiêu tiền

Xem thêm: nằm mơ thấy mình giết rắn

Sản phẩm liên quan: ngày đẹp trời để trở thành cún truyện tranh

Sản phẩm liên quan: trời xanh mây trắng

Xem thêm: c4h6 ra polibuta-1 3-dien