Tính chất của định thức

Mô tả sản phẩm

Tính chất của định thức là một chủ đề quan trọng trong đại số tuyến tính, giúp ta tính toán và biến đổi định thức một cách hiệu quả. Nắm vững các tính chất này sẽ giúp bạn giải quyết các bài toán liên quan đến ma trận và hệ phương trình tuyến tính dễ dàng hơn.

Các tính chất cơ bản của định thức

Tính chất 1: Định thức của ma trận tam giác

Định thức của một ma trận tam giác (tam giác trên hoặc tam giác dưới) bằng tích các phần tử trên đường chéo chính. Điều này giúp đơn giản hóa việc tính toán định thức của các ma trận đặc biệt này.

Tính chất 2: Ảnh hưởng của phép hoán vị hai hàng (hoặc hai cột)

Nếu hoán vị hai hàng (hoặc hai cột) của một ma trận, định thức của ma trận mới sẽ là số đối của định thức ban đầu. Tính chất này rất hữu ích trong việc biến đổi ma trận để tính toán định thức dễ dàng hơn.

Tính chất 3: Tính tuyến tính theo một hàng (hoặc một cột)

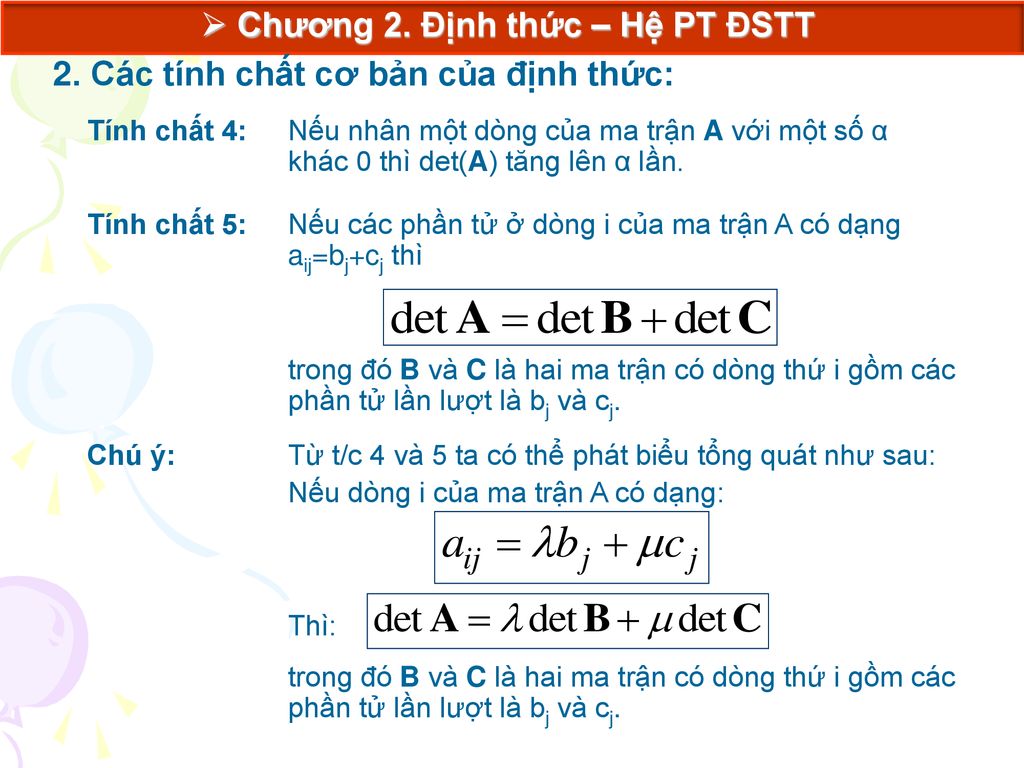
Nếu một hàng (hoặc một cột) của ma trận được nhân với một số k, thì định thức của ma trận mới sẽ bằng k lần định thức ban đầu. Ngoài ra, nếu một hàng (hoặc một cột) là tổng của hai hàng (hoặc hai cột) khác, thì định thức của ma trận đó bằng tổng các định thức của hai ma trận tương ứng, trong đó mỗi ma trận chỉ thay đổi một hàng (hoặc một cột).

Tính chất 4: Định thức của ma trận không đổi khi cộng một bội của một hàng (hoặc cột) vào một hàng (hoặc cột) khác

Đây là một tính chất rất quan trọng trong việc biến đổi ma trận về dạng tam giác để tính toán định thức dễ dàng hơn. Việc này không làm thay đổi giá trị của định thức.

Tính chất 5: Định thức của ma trận đơn vị

Định thức của ma trận đơn vị (ma trận có đường chéo chính là 1 và các phần tử khác bằng 0) luôn bằng 1.

Tính chất 6: Định thức của ma trận nghịch đảo

Nếu A là một ma trận khả nghịch, thì det(A⁻¹) = 1/det(A).

Ứng dụng của tính chất định thức

Việc hiểu và áp dụng các tính chất của định thức là rất cần thiết trong nhiều lĩnh vực như giải hệ phương trình tuyến tính, tìm ma trận nghịch đảo, tính diện tích, thể tích trong không gian nhiều chiều, và nhiều ứng dụng khác trong toán học và khoa học kỹ thuật. Bằng việc nắm vững các tính chất trên, bạn có thể tối ưu hóa quá trình tính toán và giải quyết bài toán hiệu quả hơn.

Xem thêm: điểm cực cận của mắt cận thì

Xem thêm: rau má có tác dụng gì

Sản phẩm liên quan: hình học sinh lớp 6