Tìm tập xác định của các hàm số sau
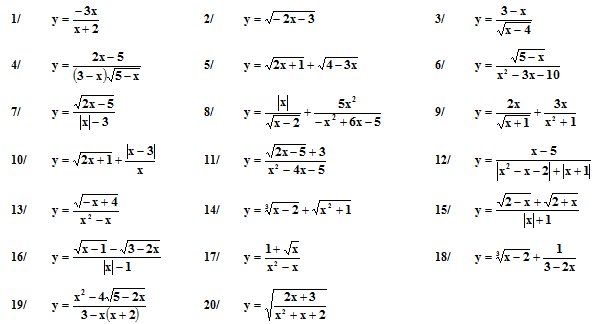
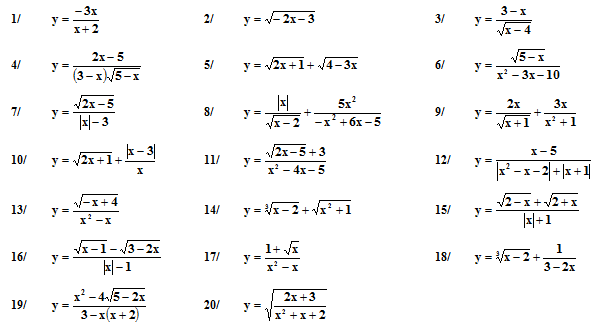
Chính Sách Vận Chuyển Và Đổi Trả Hàng
Miễn phí vận chuyển mọi đơn hàng từ 500K
- Phí ship mặc trong nước 50K
- Thời gian nhận hàng 2-3 ngày trong tuần
- Giao hàng hỏa tốc trong 24h
- Hoàn trả hàng trong 30 ngày nếu không hài lòng
Mô tả sản phẩm
Tìm tập xác định của hàm số là một bước quan trọng trong việc phân tích và vẽ đồ thị hàm số. Để tìm tập xác định, ta cần xác định các giá trị của biến số x sao cho biểu thức hàm số có nghĩa. Điều này thường liên quan đến việc loại bỏ các giá trị làm cho mẫu số bằng 0, căn thức bậc chẵn có số bị khai căn âm, hay logarit có cơ số không dương hoặc bằng 1.
Các bước tìm tập xác định của hàm số
Hàm số chứa căn thức
Để tìm tập xác định của hàm số chứa căn bậc chẵn, ta cần đảm bảo biểu thức trong căn phải không âm. Ví dụ: Cho hàm số y = √(x-2). Tập xác định của hàm số này là x - 2 ≥ 0, tương đương x ≥ 2. Vậy tập xác định là D = [2; +∞).Hàm số chứa phân thức
Đối với hàm số chứa phân thức, mẫu số không được bằng 0. Ví dụ: Cho hàm số y = 1/(x-3). Tập xác định của hàm số này là x - 3 ≠ 0, tương đương x ≠ 3. Vậy tập xác định là D = R\{3} (tập số thực trừ đi giá trị 3).Hàm số chứa logarit
Với hàm số logarit, cơ số phải dương và khác 1, và số trong logarit phải dương. Ví dụ: Cho hàm số y = log₂(x+1). Tập xác định là x + 1 > 0, tương đương x > -1. Vậy tập xác định là D = (-1; +∞).Ví dụ tổng hợp
Xét hàm số y = √(x² - 4) / (x - 1). Để hàm số có nghĩa, ta cần: * x² - 4 ≥ 0 => x ≤ -2 hoặc x ≥ 2 * x - 1 ≠ 0 => x ≠ 1 Kết hợp hai điều kiện trên, ta được tập xác định là D = (-∞; -2] ∪ [2; +∞). Tóm lại, việc xác định tập xác định của hàm số phụ thuộc vào dạng của hàm số. Cần phải xem xét kỹ các điều kiện để biểu thức hàm số có nghĩa. Việc làm chủ các kỹ thuật này là rất quan trọng để giải quyết các bài toán liên quan đến hàm số một cách chính xác.Sản phẩm liên quan: bài hội lim lớp 3
Sản phẩm liên quan: bài tập toàn thân
Xem thêm: phản xạ âm là gì
Sản phẩm liên quan: chiếc tổ của bầy ong như
Sản phẩm liên quan: quy tắc hoá trị