Ma trận khả nghịch

Mô tả sản phẩm

Một ma trận khả nghịch (hay ma trận không suy biến) là một ma trận vuông có định thức khác 0. Điều này có nghĩa là tồn tại một ma trận khác, gọi là ma trận nghịch đảo, sao cho tích của ma trận ban đầu và ma trận nghịch đảo bằng ma trận đơn vị. Việc tìm ma trận khả nghịch bao gồm kiểm tra xem định thức của ma trận có khác 0 hay không và nếu có, tính toán ma trận nghịch đảo.

Kiểm tra khả nghịch của ma trận

Tính định thức

Để xác định xem một ma trận vuông có khả nghịch hay không, bước đầu tiên là tính định thức của nó. Nếu định thức khác 0, ma trận khả nghịch. Nếu định thức bằng 0, ma trận không khả nghịch (suy biến). Có nhiều phương pháp tính định thức, tùy thuộc vào kích thước của ma trận, ví dụ như quy tắc Sarrus cho ma trận 3x3, hoặc sử dụng phép khai triển Laplace cho ma trận có kích thước lớn hơn.

Phương pháp kiểm tra khác

Ngoài việc tính định thức, ta có thể kiểm tra khả nghịch của ma trận thông qua việc kiểm tra hạng của ma trận. Nếu hạng của ma trận bằng với số chiều của ma trận, thì ma trận khả nghịch. Hạng của ma trận là số chiều lớn nhất của một không gian con được sinh bởi các cột (hay hàng) của ma trận đó.

Tính ma trận nghịch đảo

Nếu ma trận khả nghịch (định thức khác 0), ta có thể tính ma trận nghịch đảo bằng nhiều phương pháp, bao gồm:

Phương pháp sử dụng phần bù đại số

Phương pháp này liên quan đến việc tính toán ma trận phần bù đại số và chuyển vị của nó. Ma trận nghịch đảo được tính bằng công thức: A^-1 = (1/det(A)) * adj(A), trong đó det(A) là định thức của A và adj(A) là ma trận phần bù đại số của A.

Phương pháp khử Gauss-Jordan

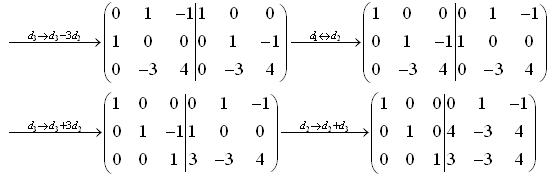
Phương pháp này hiệu quả hơn cho các ma trận lớn. Nó liên quan đến việc thực hiện các phép biến đổi hàng trên ma trận mở rộng [A | I], trong đó A là ma trận ban đầu và I là ma trận đơn vị. Sau khi thực hiện các phép biến đổi, nếu ma trận bên trái trở thành ma trận đơn vị, thì ma trận bên phải chính là ma trận nghịch đảo của A.

Sử dụng phần mềm tính toán

Nhiều phần mềm toán học như MATLAB, Mathematica, Python (với thư viện NumPy) cung cấp các hàm tích hợp để tính định thức và ma trận nghịch đảo một cách dễ dàng và hiệu quả.

Sản phẩm hữu ích: vì quá ngu si hay vì em đã yêu vội vàng lời

Xem thêm: mụn gạo ở trẻ em

Sản phẩm hữu ích: sau lũy tre làng