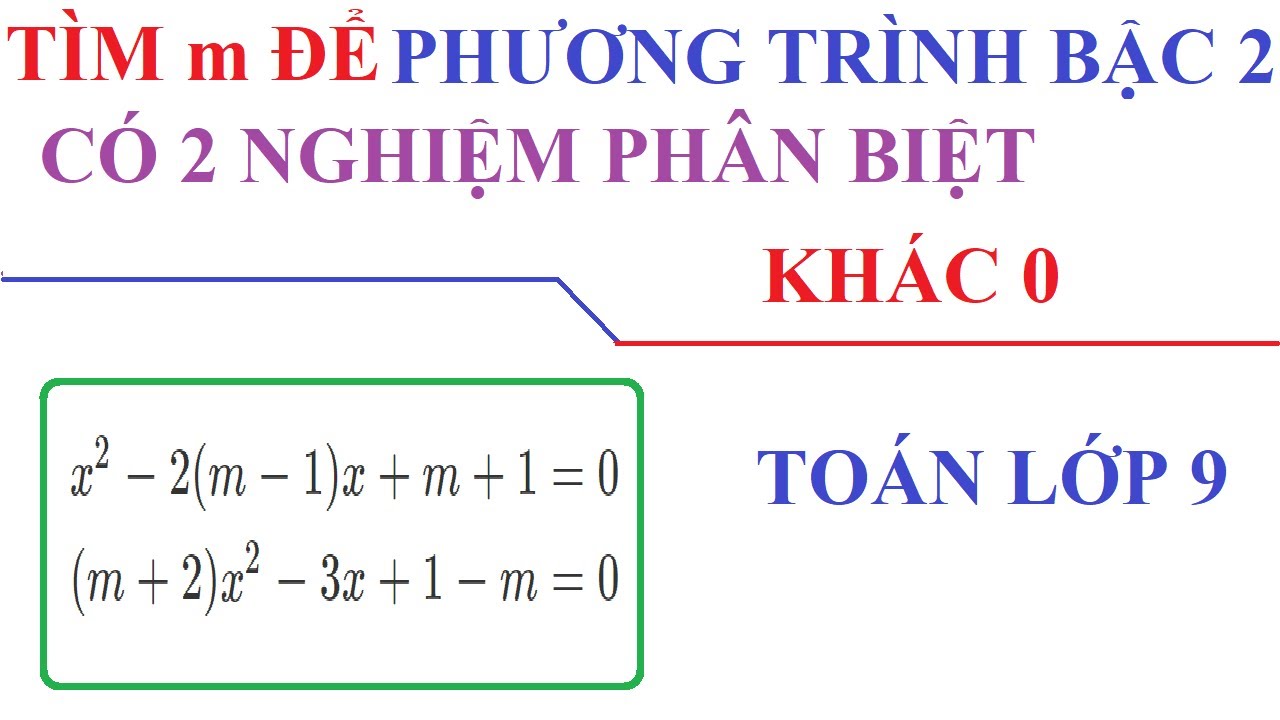
Tìm m để phương trình có 2 nghiệm phân biệt

Mô tả sản phẩm

Để phương trình có 2 nghiệm phân biệt, điều kiện là delta (hay biệt thức) của phương trình phải lớn hơn 0. Điều này phụ thuộc vào hệ số của phương trình và giá trị của tham số m. Ta cần phân tích từng trường hợp cụ thể để tìm ra điều kiện của m.

Điều kiện để phương trình bậc hai có hai nghiệm phân biệt

Phương trình bậc hai tổng quát

Phương trình bậc hai tổng quát có dạng: ax² + bx + c = 0 (với a ≠ 0).

Điều kiện để phương trình có hai nghiệm phân biệt là:

Δ = b² - 4ac > 0

Trong đó:

• a là hệ số của x²
• b là hệ số của x
• c là hệ số tự do

Áp dụng vào bài toán cụ thể

Để giải quyết bài toán tìm m để phương trình có 2 nghiệm phân biệt, bạn cần cung cấp phương trình cụ thể. Ví dụ, nếu phương trình là: x² + 2mx + m - 1 = 0, thì:

a = 1, b = 2m, c = m - 1

Áp dụng công thức delta:

Δ = (2m)² - 4(1)(m - 1) = 4m² - 4m + 4 = 4(m² - m + 1)

Để phương trình có 2 nghiệm phân biệt, ta cần:

Δ > 0 => 4(m² - m + 1) > 0

Vì m² - m + 1 = (m - 1/2)² + 3/4 luôn dương với mọi m, nên 4(m² - m + 1) luôn dương với mọi m.

Vậy, trong trường hợp này, phương trình luôn có 2 nghiệm phân biệt với mọi giá trị của m.

Lưu ý: Đây chỉ là một ví dụ. Để tìm điều kiện của m cho một phương trình cụ thể, bạn cần thay các hệ số a, b, c vào công thức delta và giải bất phương trình Δ > 0.

Xem thêm: truyện quả táo của ai

Sản phẩm liên quan: chương trình vật lý 10 mới

Xem thêm: cách làm búp bê bằng giấy