Tìm đỉnh của parabol

Mô tả sản phẩm

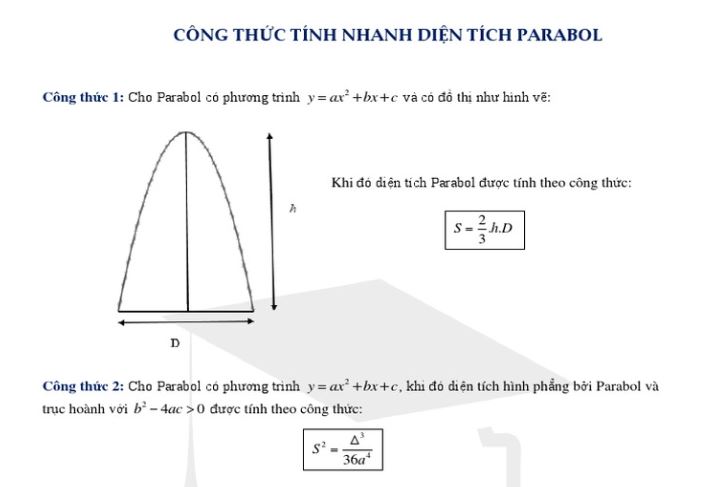
Tìm đỉnh của parabol là việc xác định tọa độ điểm cao nhất hoặc thấp nhất trên đồ thị của hàm số bậc hai. Đỉnh parabol có tọa độ là (-b/2a, -Δ/4a) với a, b là các hệ số của hàm số y = ax² + bx + c (a ≠ 0) và Δ = b² - 4ac là biệt thức delta.

Phương pháp tìm đỉnh parabol

Dùng công thức

Tọa độ đỉnh I(x_I; y_I) của parabol y = ax² + bx + c (a ≠ 0) được tính bởi công thức:

• Hoành độ đỉnh: x_I = -b/(2a)
• Tung độ đỉnh: y_I = -Δ/(4a) = - (b² - 4ac)/(4a) hoặc thay x_I vào hàm số để tính y_I = a(x_I)² + b(x_I) + c

Ví dụ: Cho hàm số y = 2x² - 4x + 3. Ta có a = 2, b = -4, c = 3. Hoành độ đỉnh: x_I = -(-4) / (2*2) = 1 Tung độ đỉnh: y_I = 2(1)² - 4(1) + 3 = 1 Vậy tọa độ đỉnh parabol là I(1; 1).

Dùng phương pháp hoàn thành bình phương

Phương pháp này giúp đưa hàm số về dạng y = a(x - h)² + k, trong đó đỉnh parabol có tọa độ (h, k). Ví dụ: y = x² - 6x + 5 Hoàn thành bình phương: y = (x² - 6x + 9) - 9 + 5 = (x - 3)² - 4 Vậy đỉnh parabol có tọa độ (3, -4).

Sử dụng máy tính bỏ túi

Một số máy tính bỏ túi có chức năng tính toán trực tiếp tọa độ đỉnh parabol. Hãy tham khảo hướng dẫn sử dụng của máy tính của bạn.

Ứng dụng của việc tìm đỉnh parabol

Việc tìm đỉnh parabol có nhiều ứng dụng trong thực tiễn, chẳng hạn như:

• Tìm giá trị lớn nhất hoặc nhỏ nhất của một hàm số
• Xác định quỹ đạo của vật thể chuyển động
• Giải các bài toán tối ưu hóa trong kinh tế, kỹ thuật

Sản phẩm hữu ích: dấu ngoặc vuông trong toán học

Xem thêm: chị google ơi hôm nay trời có mưa không

Sản phẩm hữu ích: từ có vần op

Sản phẩm hữu ích: bể nhựa nuôi cá