Tích là gì? Khám phá khái niệm tích trong toán học và ứng dụng của nó


Chính Sách Vận Chuyển Và Đổi Trả Hàng
Miễn phí vận chuyển mọi đơn hàng từ 500K
- Phí ship mặc trong nước 50K
- Thời gian nhận hàng 2-3 ngày trong tuần
- Giao hàng hỏa tốc trong 24h
- Hoàn trả hàng trong 30 ngày nếu không hài lòng
Mô tả sản phẩm
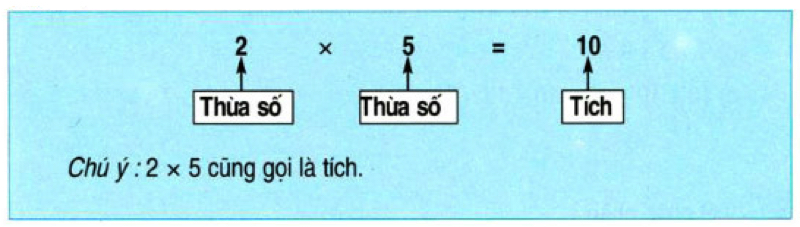
Tích, trong toán học, là kết quả của phép nhân giữa hai hoặc nhiều số. Ví dụ, tích của 2 và 3 là 6 (2 x 3 = 6). Hiểu rõ khái niệm tích là nền tảng quan trọng cho việc học toán ở mọi cấp độ.
Khái niệm Tích trong Toán học
Tích của hai số
Tích của hai số a và b được ký hiệu là a × b hoặc a * b hoặc ab (khi không có dấu hiệu nhầm lẫn). Kết quả của phép nhân này cho ta tích của hai số đó. Ví dụ: tích của 5 và 7 là 35 (5 × 7 = 35). Phép nhân có tính chất giao hoán (a × b = b × a) và kết hợp ((a × b) × c = a × (b × c)). Điều này có nghĩa là thứ tự nhân các số không ảnh hưởng đến kết quả cuối cùng.Tích của nhiều số
Khái niệm tích có thể mở rộng cho nhiều hơn hai số. Tích của ba số a, b và c là (a × b) × c hoặc a × (b × c), đều cho ra cùng một kết quả. Ta có thể nhân các số theo bất kỳ thứ tự nào mà vẫn cho ra cùng một tích. Ví dụ: tích của 2, 3 và 4 là 24 (2 × 3 × 4 = 24).Tính chất của phép nhân và tích
Phép nhân có một số tính chất quan trọng ảnh hưởng đến tích:- Tính chất giao hoán: a × b = b × a
- Tính chất kết hợp: (a × b) × c = a × (b × c)
- Tính chất phân phối: a × (b + c) = a × b + a × c
- Nhân với 0: a × 0 = 0
- Nhân với 1: a × 1 = a
Ứng dụng của Tích trong cuộc sống
Tích không chỉ đơn thuần là một khái niệm toán học mà còn có ứng dụng rộng rãi trong nhiều lĩnh vực của cuộc sống:Trong kinh tế
Tích được sử dụng để tính toán doanh thu, lợi nhuận, và nhiều chỉ số kinh tế khác. Ví dụ, để tính tổng doanh thu, ta nhân số lượng sản phẩm bán được với giá bán của mỗi sản phẩm.Trong khoa học
Trong vật lý, tích được sử dụng để tính toán công, động năng, thế năng và nhiều đại lượng vật lý khác. Trong hóa học, tích được sử dụng trong các phép tính liên quan đến nồng độ, khối lượng mol, v.v.Trong kỹ thuật
Trong kỹ thuật, tích được sử dụng trong các phép tính liên quan đến diện tích, thể tích, lực, momen, và nhiều đại lượng kỹ thuật khác. Ví dụ, tính diện tích hình chữ nhật bằng cách nhân chiều dài với chiều rộng.Trong đời sống hàng ngày
Ngay cả trong đời sống hàng ngày, chúng ta cũng thường xuyên sử dụng tích mà không hề nhận ra. Ví dụ, tính tổng số tiền cần trả khi mua nhiều sản phẩm cùng loại, tính số lượng sản phẩm cần thiết cho một dự án, hay tính toán thời gian cần thiết cho một công việc.Mở rộng khái niệm Tích
Khái niệm tích không chỉ giới hạn ở các số nguyên hay số thực. Nó còn được mở rộng đến các số phức, ma trận, và các cấu trúc toán học khác phức tạp hơn. Trong đại số tuyến tính, tích của ma trận là một phép toán quan trọng, được sử dụng rộng rãi trong giải quyết các hệ phương trình tuyến tính và nhiều bài toán khác.Tích vô hướng và tích có hướng
Trong vector, ta có khái niệm tích vô hướng và tích có hướng. Tích vô hướng cho ra một số, trong khi tích có hướng cho ra một vector khác. Đây là những khái niệm quan trọng trong vật lý và kỹ thuật.Tích phân
Trong giải tích, tích phân là một khái niệm liên quan đến tích. Nó được sử dụng để tính diện tích dưới đường cong, thể tích của vật thể, và nhiều đại lượng khác.Kết luận
Tích là một khái niệm cơ bản nhưng vô cùng quan trọng trong toán học và có ứng dụng rộng rãi trong nhiều lĩnh vực khác nhau của cuộc sống. Hiểu rõ khái niệm tích và các tính chất của phép nhân là nền tảng để học tập và áp dụng toán học hiệu quả. Việc nắm vững khái niệm này sẽ giúp bạn giải quyết được nhiều bài toán phức tạp và ứng dụng nó vào thực tiễn một cách dễ dàng.Sản phẩm liên quan: tóc đẹp cho học sinh nữ cấp 2 mặt tròn
Xem thêm: thu hoạch lúa vào tháng mấy
Sản phẩm hữu ích: tóc ngắn cho mặt to vuông