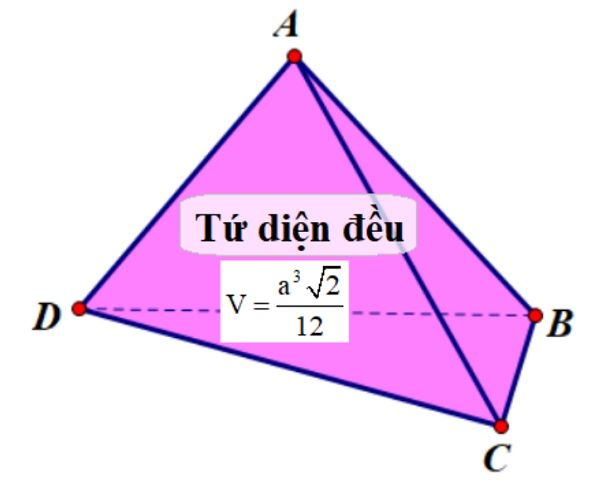
Thể tích tứ diện
Chính Sách Vận Chuyển Và Đổi Trả Hàng
Miễn phí vận chuyển mọi đơn hàng từ 500K
- Phí ship mặc trong nước 50K
- Thời gian nhận hàng 2-3 ngày trong tuần
- Giao hàng hỏa tốc trong 24h
- Hoàn trả hàng trong 30 ngày nếu không hài lòng
Mô tả sản phẩm
Thể tích của một tứ diện được tính bằng công thức: V = (1/6)|a.(b x c)|, trong đó a, b, c là các vector tạo thành ba cạnh của tứ diện cùng xuất phát từ một đỉnh. Công thức này dựa trên tích hỗn hợp của ba vector. Ngoài ra, còn có các công thức khác để tính thể tích tứ diện tùy thuộc vào dữ liệu đã cho.
Các công thức tính thể tích tứ diện
Công thức dựa trên tọa độ đỉnh
Giả sử tứ diện ABCD có các đỉnh A(xA, yA, zA), B(xB, yB, zB), C(xC, yC, zC), D(xD, yD, zD). Thể tích tứ diện được tính bằng: V = (1/6)|det(M)| với M là ma trận:| xA yA zA 1 | | xB yB zB 1 | | xC yC zC 1 | | xD yD zD 1 |det(M) là định thức của ma trận M. Công thức này rất hữu ích khi ta biết tọa độ các đỉnh của tứ diện.
Công thức dựa trên diện tích đáy và chiều cao
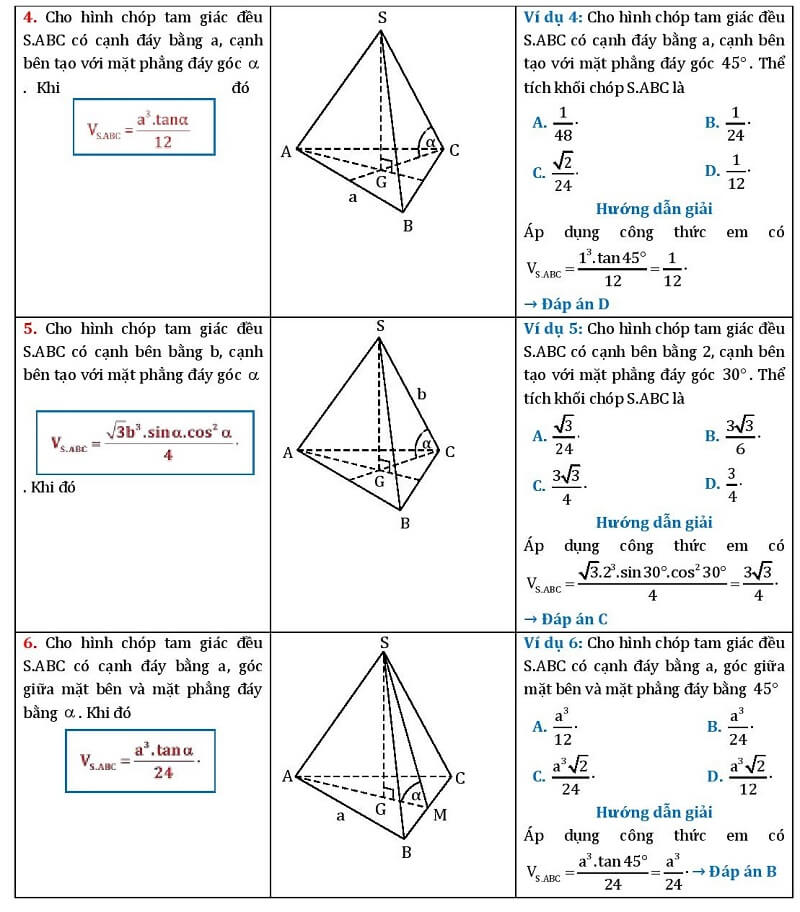
Thể tích của tứ diện cũng có thể tính bằng công thức: V = (1/3) * S * h Trong đó: * S là diện tích của một mặt của tứ diện (đáy). * h là chiều cao tương ứng với mặt đáy đó. Công thức này tương tự như công thức tính thể tích của hình chóp. Tuy nhiên, việc xác định chiều cao h có thể phức tạp hơn so với các hình chóp thông thường.Công thức dựa trên tích vô hướng và tích vectơ
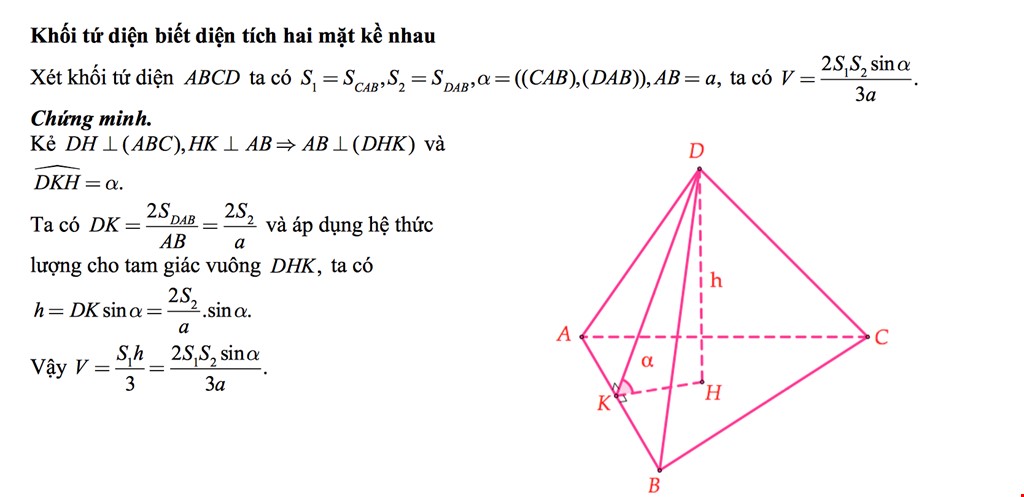
Như đã đề cập ở đầu bài viết, thể tích tứ diện cũng có thể được tính bằng công thức sử dụng tích vô hướng và tích vectơ: V = (1/6)|a.(b x c)|, trong đó a, b, c là ba vector cạnh của tứ diện. Công thức này thường được sử dụng trong các bài toán hình học không gian phức tạp. Việc lựa chọn công thức phù hợp phụ thuộc vào dữ liệu đã cho trong bài toán.Sản phẩm hữu ích: cho rùa ăn bao nhiêu là đủ
Sản phẩm hữu ích: phiếu bài tập tiếng việt lớp 3 chân trời sáng tạo
Sản phẩm hữu ích: tấm cám búp bê
Xem thêm: văn tả người thân trong gia đình