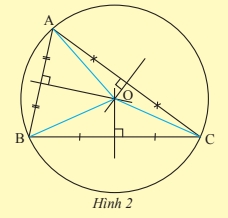
Tam giác ABC nội tiếp đường tròn
Chính Sách Vận Chuyển Và Đổi Trả Hàng
Miễn phí vận chuyển mọi đơn hàng từ 500K
- Phí ship mặc trong nước 50K
- Thời gian nhận hàng 2-3 ngày trong tuần
- Giao hàng hỏa tốc trong 24h
- Hoàn trả hàng trong 30 ngày nếu không hài lòng
Mô tả sản phẩm
Tam giác ABC nội tiếp đường tròn là một tam giác có ba đỉnh A, B, C nằm trên cùng một đường tròn. Điều này có nghĩa là tồn tại một đường tròn đi qua cả ba đỉnh của tam giác. Đường tròn này được gọi là đường tròn ngoại tiếp tam giác ABC.
Tính chất của tam giác ABC nội tiếp đường tròn
Góc nội tiếp và góc ở tâm
Góc nội tiếp là góc có đỉnh nằm trên đường tròn và hai cạnh chứa hai dây cung của đường tròn. Góc ở tâm là góc có đỉnh trùng với tâm của đường tròn và hai cạnh chứa hai bán kính. Một tính chất quan trọng là góc nội tiếp chắn một cung sẽ bằng một nửa góc ở tâm chắn cùng cung đó. Ví dụ, nếu góc nội tiếp ∠BAC chắn cung BC, và góc ở tâm ∠BOC chắn cung BC, thì ∠BAC = 1/2 ∠BOC.Định lý Thales
Định lý Thales là một trường hợp đặc biệt của tam giác nội tiếp đường tròn. Nó khẳng định rằng nếu một đường thẳng đi qua một điểm trên đường tròn và vuông góc với đường kính tại điểm đó, thì đường thẳng đó sẽ tiếp xúc với đường tròn tại điểm đó.Các đường trong tam giác nội tiếp
Trong một tam giác nội tiếp đường tròn, ta có thể tìm được nhiều đường quan trọng, bao gồm đường tròn ngoại tiếp (đã đề cập ở trên), đường tròn nội tiếp (tiếp xúc với ba cạnh của tam giác), và các đường tròn bàng tiếp (tiếp xúc với một cạnh và hai phần kéo dài của hai cạnh còn lại). Vị trí của các tâm đường tròn này có liên hệ chặt chẽ với các yếu tố hình học của tam giác.Ứng dụng
Hiểu về tam giác nội tiếp đường tròn rất quan trọng trong nhiều lĩnh vực toán học, đặc biệt là hình học phẳng, lượng giác và giải tích. Nó cũng được ứng dụng trong các lĩnh vực khác như vật lý, kỹ thuật và thiết kế.Sản phẩm hữu ích: nguyên liệu điều chế hidro trong phòng thí nghiệm
Sản phẩm liên quan: kim loại tác dụng với phi kim
Sản phẩm liên quan: kí tự vô cực
Xem thêm: toán xác suất thống kê lớp 11