Soạn Bài Đi Đường Ngắn Nhất

Mô tả sản phẩm

Soạn bài đi đường ngắn nhất thường bao gồm việc tìm hiểu khái niệm đồ thị, thuật toán Dijkstra hoặc thuật toán A*, và cách áp dụng chúng để tìm đường đi ngắn nhất giữa hai điểm. Bài viết này sẽ hướng dẫn bạn cách soạn bài một cách hiệu quả và dễ hiểu.

Khái niệm đồ thị và thuật toán tìm đường ngắn nhất

Đồ thị

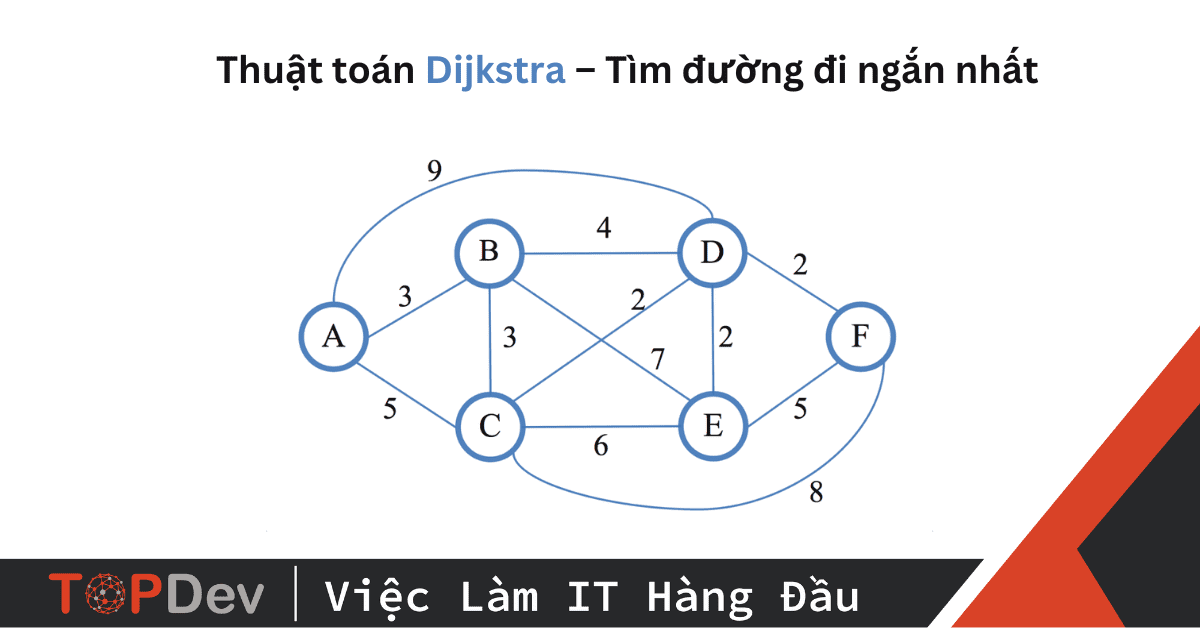
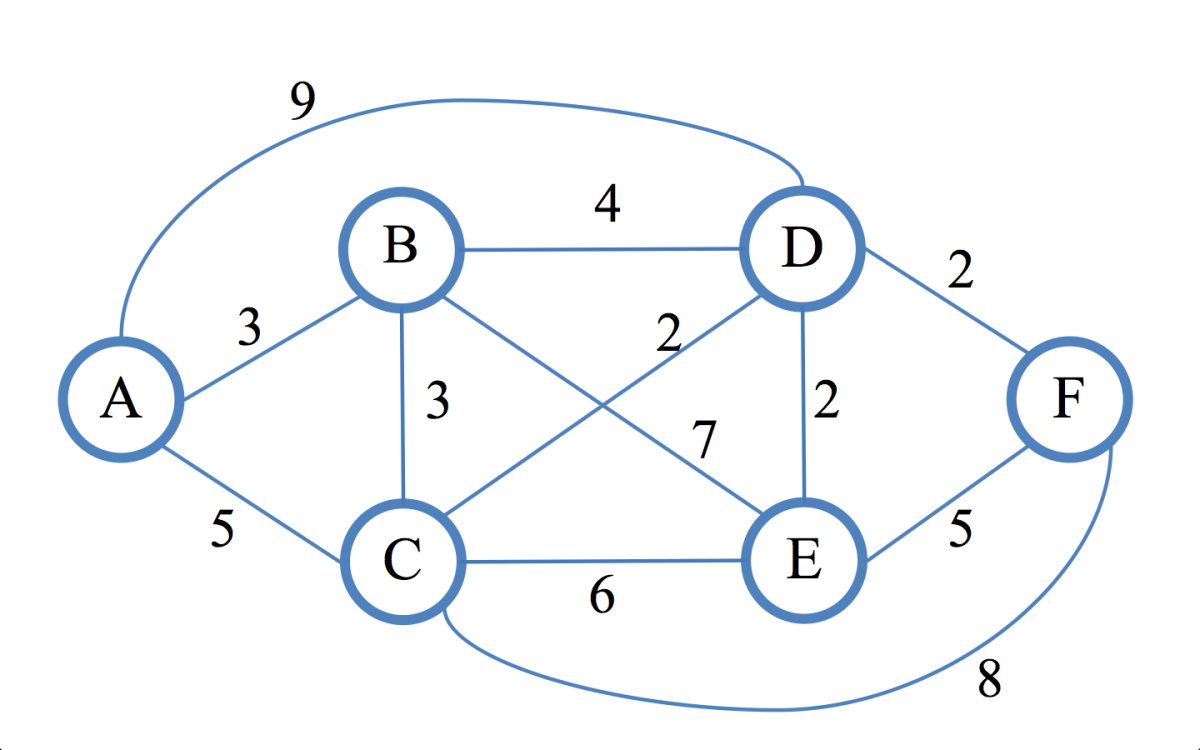
Đồ thị là một cấu trúc dữ liệu bao gồm các đỉnh (node) và các cạnh (edge) kết nối các đỉnh với nhau. Trong bài toán tìm đường ngắn nhất, các đỉnh có thể là các giao điểm trên bản đồ, còn các cạnh là các đoạn đường nối giữa các giao điểm. Chiều dài của mỗi cạnh thường được biểu diễn bằng trọng số (weight), ví dụ như khoảng cách thực tế giữa hai giao điểm.

Thuật toán Dijkstra

Thuật toán Dijkstra là một thuật toán tìm đường đi ngắn nhất từ một đỉnh nguồn đến tất cả các đỉnh khác trong một đồ thị có trọng số không âm. Thuật toán này hoạt động bằng cách duyệt đồ thị từng bước, cập nhật khoảng cách ngắn nhất từ đỉnh nguồn đến các đỉnh khác.

Thuật toán A*

Thuật toán A* là một thuật toán tìm đường đi ngắn nhất được sử dụng rộng rãi trong các trò chơi và hệ thống định vị. Nó là một thuật toán tìm kiếm heuristic, nghĩa là nó sử dụng một hàm heuristic để ước lượng khoảng cách từ một đỉnh đến đỉnh đích. Điều này giúp thuật toán A* tìm kiếm hiệu quả hơn thuật toán Dijkstra trong nhiều trường hợp.

Cách áp dụng để tìm đường đi ngắn nhất

Để áp dụng các thuật toán này vào bài toán thực tế, bạn cần biểu diễn bản đồ dưới dạng đồ thị, sau đó sử dụng một trong các thuật toán trên để tìm đường đi ngắn nhất. Có nhiều công cụ và thư viện lập trình hỗ trợ việc này, giúp bạn đơn giản hóa quá trình soạn bài. Việc hiểu rõ nguyên lý hoạt động của các thuật toán sẽ giúp bạn giải quyết các bài toán phức tạp hơn một cách hiệu quả. Hãy thực hành nhiều ví dụ để nắm vững kiến thức.

Xem thêm: nhật ký vợ chồng hài hòa

Xem thêm: soạn văn 8 câu trần thuật ngắn nhất

Xem thêm: lô hay về ngày thứ 2