Sơ Đồ Hình Học Lớp 8

Mô tả sản phẩm

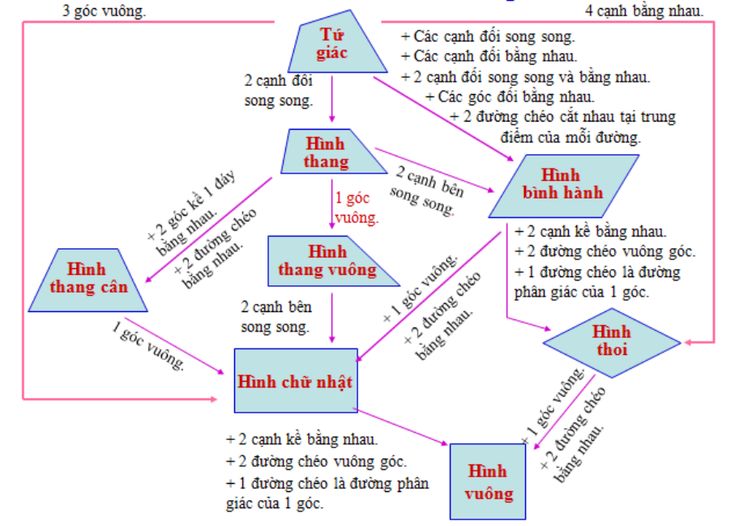
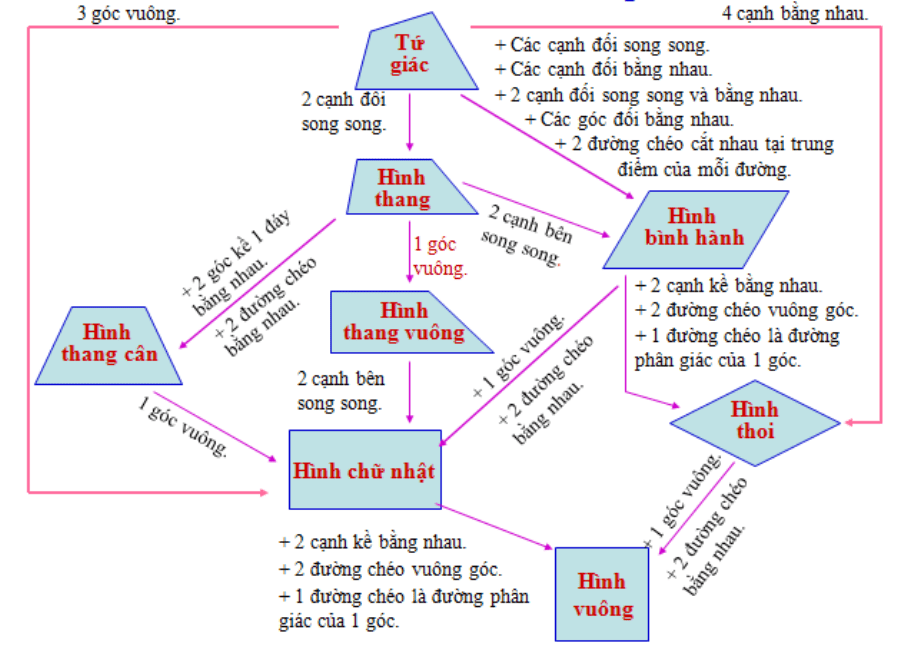
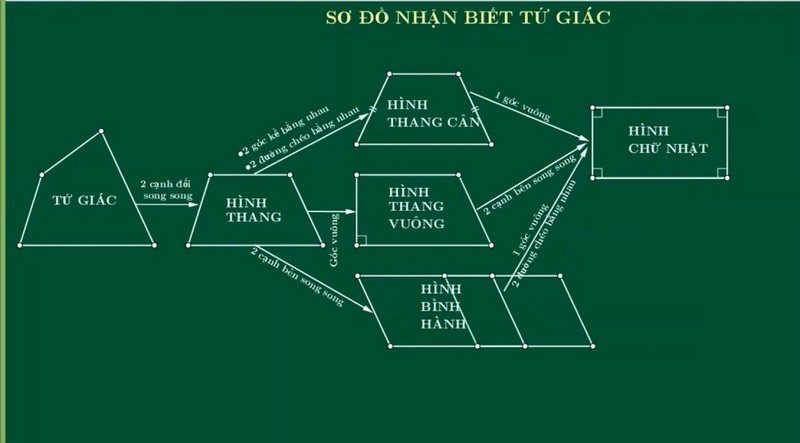
Sơ đồ hình học lớp 8 tổng hợp kiến thức trọng tâm của chương trình hình học lớp 8, giúp bạn hệ thống lại kiến thức một cách dễ hiểu và nhanh chóng. Bài viết này sẽ cung cấp cho bạn một bản tóm tắt chi tiết, bao gồm các định lý, tính chất, công thức và ví dụ minh họa.

Chương 1: Tứ Giác

1.1 Hình thang:

Định nghĩa, tính chất, dấu hiệu nhận biết, hình thang cân, diện tích hình thang. Ví dụ: Tính diện tích hình thang có đáy lớn 10cm, đáy nhỏ 6cm, chiều cao 4cm.

1.2 Hình bình hành:

Định nghĩa, tính chất, dấu hiệu nhận biết, diện tích hình bình hành. Ví dụ: Một hình bình hành có hai cạnh kề bằng 5cm và 8cm, góc giữa hai cạnh đó bằng 60 độ. Tính diện tích hình bình hành.

1.3 Hình chữ nhật:

Định nghĩa, tính chất, dấu hiệu nhận biết, diện tích hình chữ nhật. Ví dụ: Một hình chữ nhật có chiều dài 12cm, chiều rộng 8cm. Tính diện tích và chu vi hình chữ nhật.

1.4 Hình thoi:

Định nghĩa, tính chất, dấu hiệu nhận biết, diện tích hình thoi. Ví dụ: Một hình thoi có độ dài hai đường chéo là 6cm và 8cm. Tính diện tích hình thoi.

1.5 Hình vuông:

Định nghĩa, tính chất, diện tích hình vuông. Ví dụ: Một hình vuông có cạnh bằng 5cm. Tính diện tích và chu vi hình vuông.

Chương 2: Tam Giác

2.1 Các trường hợp bằng nhau của tam giác:

Trình bày các trường hợp bằng nhau của tam giác (c.c.c, c.g.c, g.c.g, g.c.g) và các ví dụ minh họa.

2.2 Đường trung bình của tam giác:

Định nghĩa, tính chất đường trung bình của tam giác và ứng dụng. Ví dụ: Tìm độ dài đường trung bình của tam giác biết độ dài cạnh đáy.

2.3 Các đường đồng quy trong tam giác:

Ba đường trung tuyến, ba đường phân giác, ba đường cao, ba đường trung trực và điểm đồng quy của chúng.

Chương 3: Định lý Pytago

3.1 Định lý Pytago:

Phát biểu, chứng minh và ứng dụng định lý Pytago trong việc tính toán độ dài cạnh của tam giác vuông. Ví dụ: Tính độ dài cạnh huyền của tam giác vuông có hai cạnh góc vuông bằng 3cm và 4cm.

3.2 Định lý đảo của Pytago:

Phát biểu và ứng dụng định lý đảo của Pytago để chứng minh một tam giác là tam giác vuông. Bài viết này chỉ là một sơ đồ tổng quan về hình học lớp 8. Để hiểu sâu hơn, bạn cần tham khảo thêm sách giáo khoa và các tài liệu bổ trợ khác. Chúc bạn học tốt!

Sản phẩm hữu ích: rô to là gì

Xem thêm: sự ngưng tụ là gì

Xem thêm: cách giâm cành hoa hồng bằng b1