Quy tắc 3 điểm vectơ

Mô tả sản phẩm

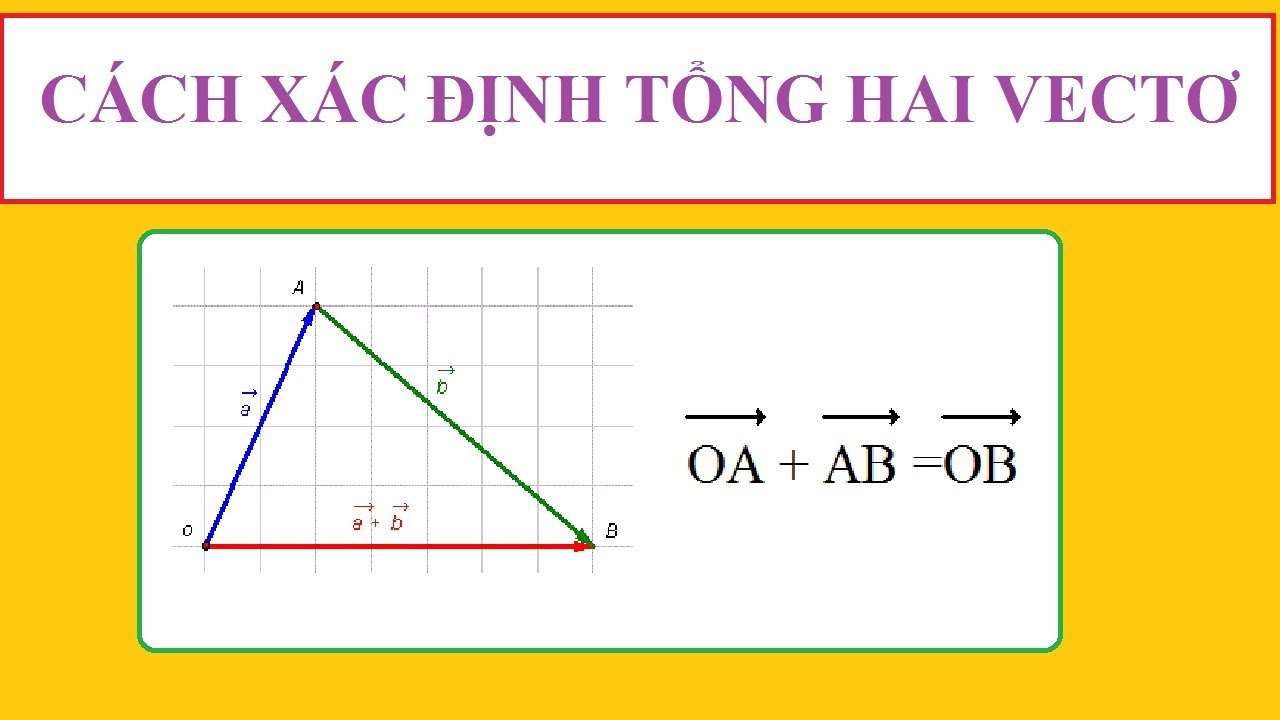
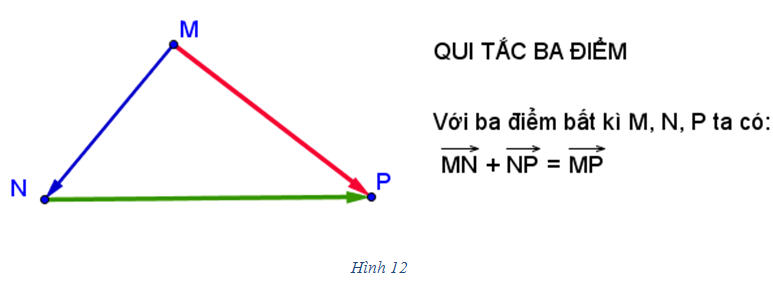
Quy tắc 3 điểm vectơ là một phương pháp xác định vectơ tổng của hai vectơ bằng cách sử dụng quy tắc hình bình hành hoặc quy tắc tam giác. Cụ thể, nếu có hai vectơ $\vec{a}$ và $\vec{b}$, vectơ tổng $\vec{a} + \vec{b}$ được xác định bằng cách nối điểm cuối của $\vec{a}$ với điểm đầu của $\vec{b}$, hoặc ngược lại, tạo thành một tam giác. Vectơ tổng sẽ là vectơ nối điểm đầu của $\vec{a}$ với điểm cuối của $\vec{b}$.

Hiểu rõ quy tắc 3 điểm vectơ

Quy tắc hình bình hành:

Trong quy tắc hình bình hành, ta đặt hai vectơ $\vec{a}$ và $\vec{b}$ sao cho chúng có chung điểm gốc O. Vectơ tổng $\vec{a} + \vec{b}$ chính là đường chéo của hình bình hành tạo bởi hai vectơ này. Phương pháp này trực quan và dễ hình dung.

Quy tắc tam giác:

Quy tắc tam giác cho phép ta xác định vectơ tổng bằng cách đặt liên tiếp hai vectơ. Đầu tiên, ta vẽ vectơ $\vec{a}$. Sau đó, từ điểm cuối của $\vec{a}$, ta vẽ vectơ $\vec{b}$. Vectơ tổng $\vec{a} + \vec{b}$ chính là vectơ nối từ điểm đầu của $\vec{a}$ đến điểm cuối của $\vec{b}$. Đây là cách tiếp cận đơn giản và thường được sử dụng để chứng minh nhiều tính chất của vectơ.

Ứng dụng của quy tắc 3 điểm vectơ

Quy tắc 3 điểm vectơ có nhiều ứng dụng quan trọng trong toán học và vật lý, bao gồm:

Trong cơ học:

Quy tắc này được sử dụng để tính tổng hợp lực, vận tốc và gia tốc của các vật thể. Việc biểu diễn các đại lượng vật lý dưới dạng vectơ và sử dụng quy tắc 3 điểm vectơ giúp giải quyết các bài toán phức tạp một cách dễ dàng hơn.

Trong hình học:

Quy tắc 3 điểm vectơ là nền tảng để chứng minh nhiều định lý hình học, ví dụ như định lý về trọng tâm của tam giác.

Tổng kết

Quy tắc 3 điểm vectơ là một công cụ hữu ích và quan trọng trong toán học và vật lý. Việc hiểu rõ quy tắc này giúp giải quyết các bài toán liên quan đến vectơ một cách hiệu quả và chính xác. Hiểu được cả hai cách tiếp cận (hình bình hành và tam giác) sẽ giúp bạn linh hoạt hơn trong việc áp dụng quy tắc này vào các bài toán khác nhau.

Sản phẩm liên quan: cách trị bọ chó dân gian

Sản phẩm hữu ích: trong hệ si đơn vị của cường độ dòng điện là

Xem thêm: tóc có dẫn điện không

Sản phẩm hữu ích: dao ghép cây nhật bãi

Sản phẩm liên quan: test tốc độ đọc sách