Phương trình quy về phương trình bậc hai


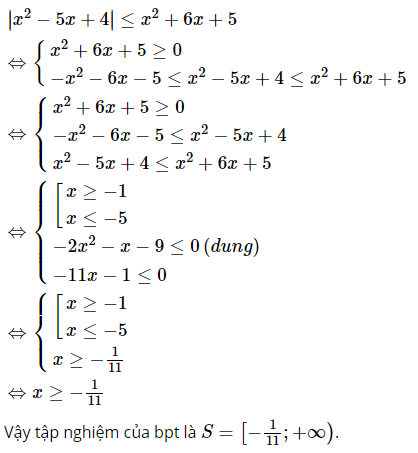
Chính Sách Vận Chuyển Và Đổi Trả Hàng
Miễn phí vận chuyển mọi đơn hàng từ 500K
- Phí ship mặc trong nước 50K
- Thời gian nhận hàng 2-3 ngày trong tuần
- Giao hàng hỏa tốc trong 24h
- Hoàn trả hàng trong 30 ngày nếu không hài lòng
Mô tả sản phẩm
Phương trình quy về phương trình bậc hai là những phương trình không phải là phương trình bậc hai nhưng có thể biến đổi tương đương về dạng phương trình bậc hai ax² + bx + c = 0 (với a ≠ 0). Việc biến đổi này giúp ta giải quyết dễ dàng hơn bằng cách sử dụng công thức nghiệm hoặc phương pháp khác dành cho phương trình bậc hai.
Các dạng phương trình quy về phương trình bậc hai
Phương trình chứa căn thức
Nhiều phương trình chứa căn thức có thể được giải quyết bằng cách bình phương hai vế để loại bỏ căn thức, dẫn đến một phương trình bậc hai hoặc phương trình quy về bậc hai. Tuy nhiên, cần chú ý kiểm tra nghiệm sau khi giải, vì bình phương hai vế có thể dẫn đến nghiệm ngoại lai.
Phương trình phân thức
Một số phương trình phân thức có thể được quy về phương trình bậc hai bằng cách khử mẫu, quy đồng mẫu số và rút gọn biểu thức. Lưu ý điều kiện xác định của phương trình để loại bỏ nghiệm ngoại lai.
Phương trình tích
Phương trình dạng tích (A(x).B(x) = 0) trong đó A(x) và B(x) là các biểu thức chứa x, có thể được giải bằng cách giải từng phương trình A(x) = 0 và B(x) = 0. Nếu các phương trình này quy về phương trình bậc hai, ta giải chúng bằng công thức nghiệm.
Phương trình chứa dấu giá trị tuyệt đối
Phương trình chứa dấu giá trị tuyệt đối |f(x)| = g(x) có thể được giải bằng cách xét các trường hợp khác nhau tùy thuộc vào dấu của f(x). Mỗi trường hợp có thể dẫn đến một hoặc nhiều phương trình bậc hai.
Cách giải phương trình quy về phương trình bậc hai
Bước 1: Biến đổi phương trình về dạng phương trình bậc hai chuẩn ax² + bx + c = 0. Bước này thường bao gồm các thao tác như: khử mẫu, bình phương hai vế, phân tích nhân tử, sử dụng các hằng đẳng thức đáng nhớ. Bước 2: Giải phương trình bậc hai bằng công thức nghiệm hoặc phương pháp khác (phân tích thành nhân tử, tìm nghiệm nguyên...). Bước 3: Kiểm tra điều kiện và loại bỏ nghiệm ngoại lai (nếu có).
Ví dụ
Giải phương trình: √(x+2) + √(2-x) = 2. Bình phương hai vế, ta được: (x+2) + 2√((x+2)(2-x)) + (2-x) = 4. Rút gọn, ta có: 2√(4-x²) = 0. => 4 - x² = 0 => x = ±2. Kiểm tra điều kiện: x = 2 thỏa mãn, x = -2 thỏa mãn. Vậy nghiệm của phương trình là x = 2 và x = -2.
Sản phẩm liên quan: các bộ phận của con dê
Sản phẩm liên quan: công thức toán 10 kết nối tri thức
Sản phẩm liên quan: tiếng chào mào vàng