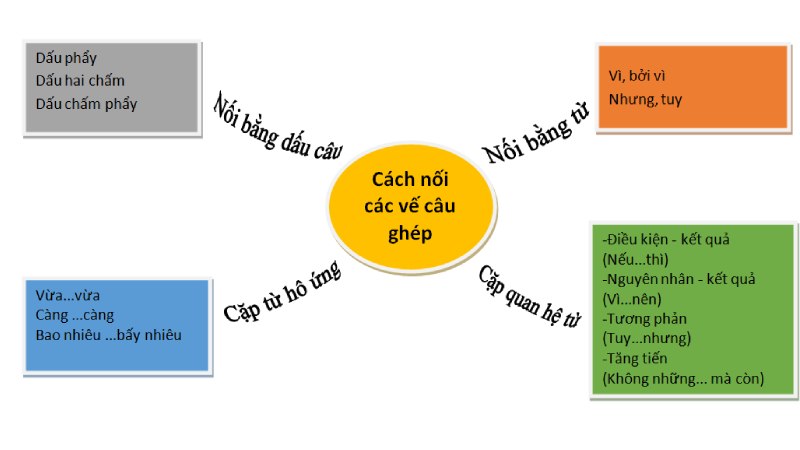
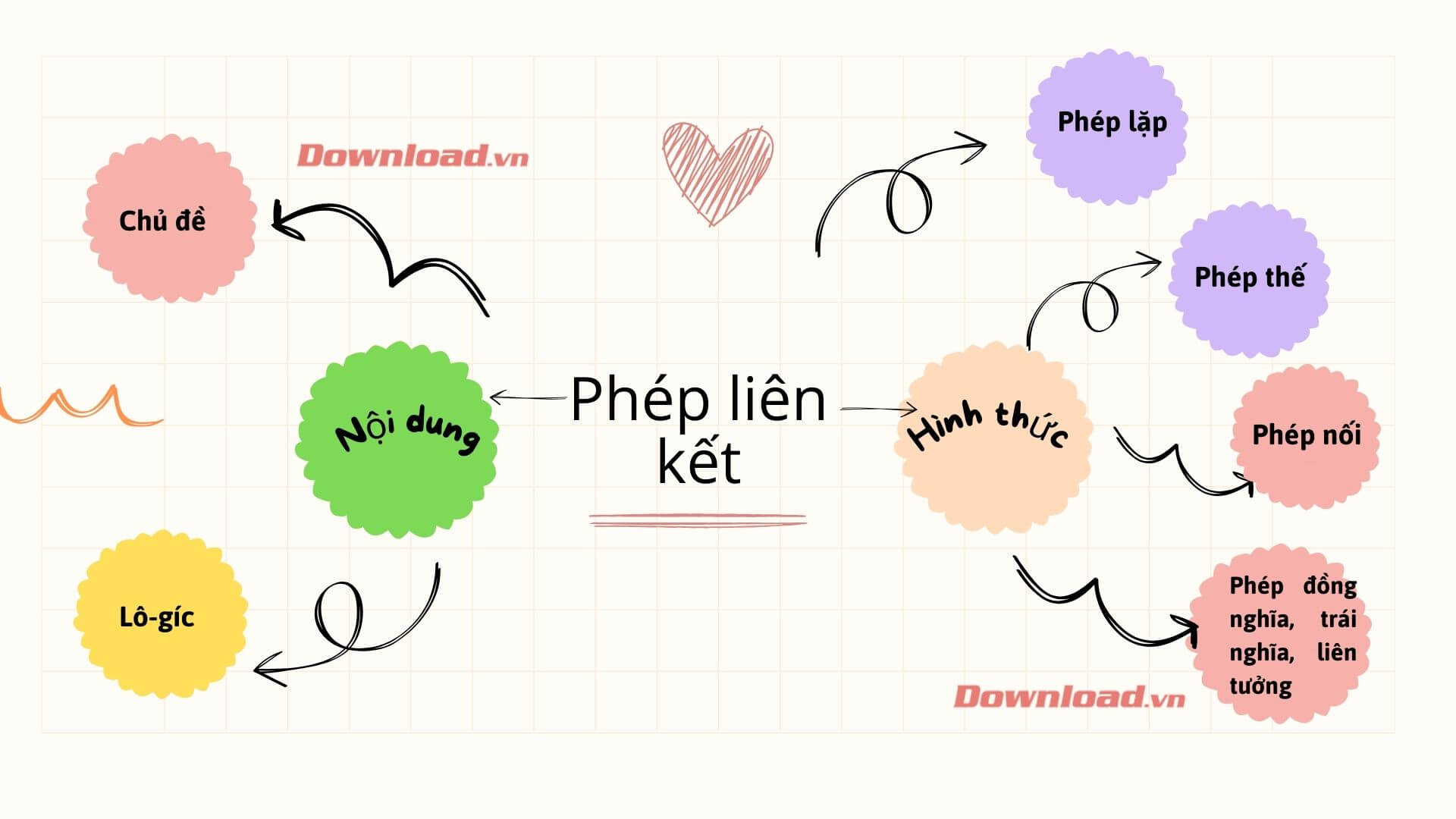
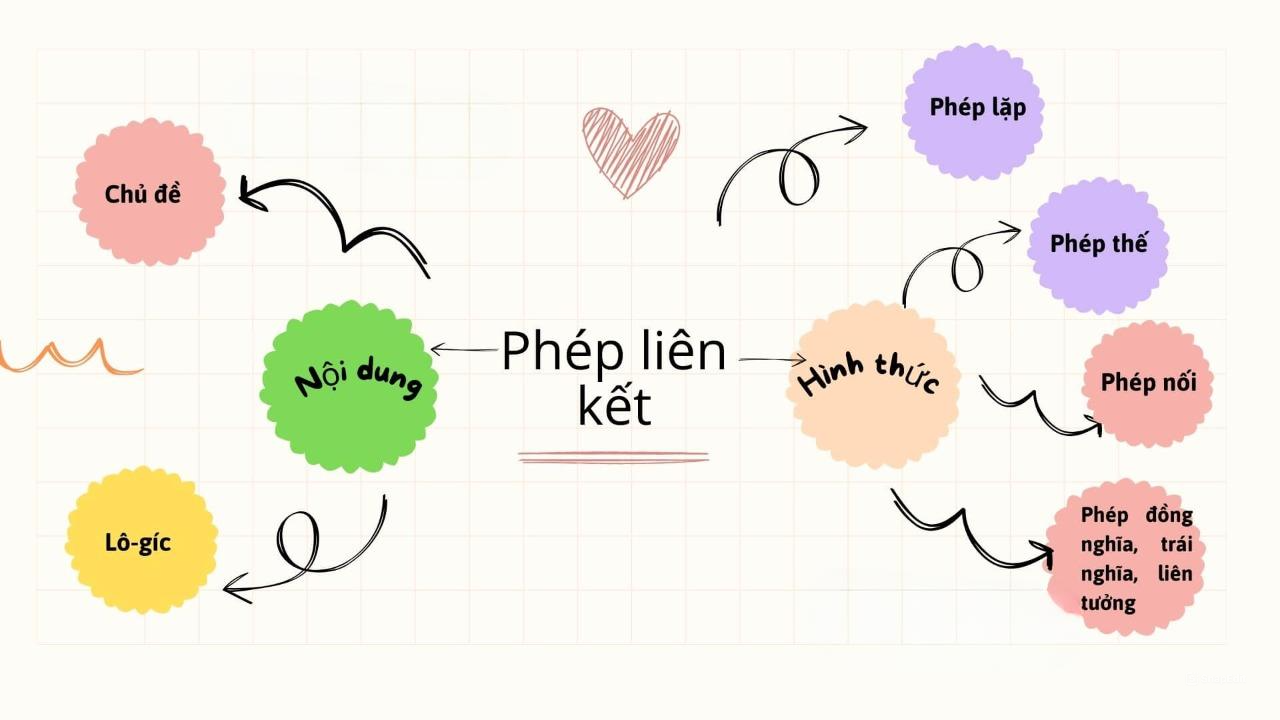
Phép Liên Kết Hình Thức Là Gì?

Mô tả sản phẩm

Phép liên kết hình thức là một phép toán trong đại số tuyến tính dùng để biểu diễn mối quan hệ tuyến tính giữa các vectơ. Nói một cách đơn giản, nó cho phép ta kiểm tra xem liệu một vectơ có thể được biểu diễn như là tổ hợp tuyến tính của các vectơ khác hay không.

Khái niệm cơ bản về phép liên kết hình thức

Tổ hợp tuyến tính

Trước khi hiểu phép liên kết hình thức, ta cần hiểu về tổ hợp tuyến tính. Tổ hợp tuyến tính của một tập hợp các vectơ {v₁, v₂, ..., v_n} là một biểu thức dạng: c₁v₁ + c₂v₂ + ... + c_nv_n, trong đó c₁, c₂, ..., c_n là các số vô hướng (thường là số thực hoặc số phức).

Phép liên kết hình thức và ma trận

Phép liên kết hình thức thường được biểu diễn dưới dạng ma trận. Cho một tập hợp các vectơ {v₁, v₂, ..., v_n} và một vectơ w, ta muốn kiểm tra xem liệu w có thể được biểu diễn như một tổ hợp tuyến tính của {v₁, v₂, ..., v_n} hay không. Điều này tương đương với việc giải hệ phương trình tuyến tính Ax = w, trong đó A là ma trận có các cột là các vectơ v₁, v₂, ..., v_n, và x là vectơ cột chứa các hệ số c₁, c₂, ..., c_n.

Ứng dụng của phép liên kết hình thức

Phép liên kết hình thức có nhiều ứng dụng quan trọng trong toán học và các lĩnh vực liên quan, chẳng hạn như:

• Xác định độc lập tuyến tính của các vectơ.
• Tìm không gian con sinh bởi một tập hợp các vectơ.
• Giải các hệ phương trình tuyến tính.
• Trong đồ họa máy tính để tính toán các phép biến đổi hình học.
• Trong máy học để phân tích dữ liệu và xây dựng mô hình.

Tóm lại, phép liên kết hình thức là một công cụ quan trọng trong đại số tuyến tính, cho phép chúng ta phân tích và hiểu mối quan hệ giữa các vectơ. Việc nắm vững khái niệm này là nền tảng cho việc học tập và ứng dụng nhiều lĩnh vực khác.

Sản phẩm hữu ích: việt cộng là gì

Sản phẩm hữu ích: 5 chén trên bàn thờ gia tiên đựng gì

Sản phẩm hữu ích: từ đồng nghĩa với lãng phí

Sản phẩm hữu ích: tiểu nhân là gì

Sản phẩm liên quan: khí metan kí hiệu là gì