Công thức Nhị Thức Newton
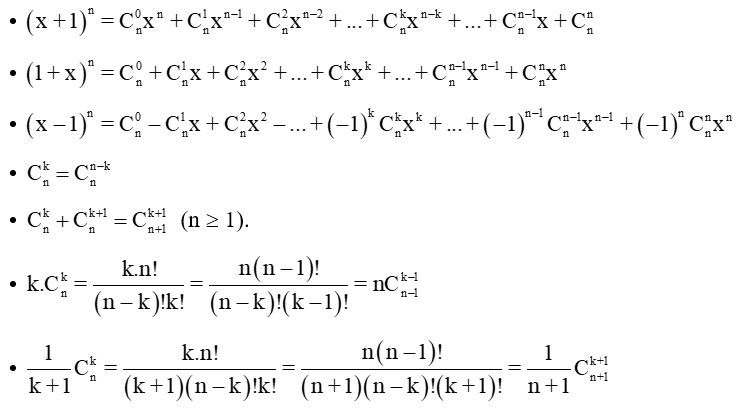

Chính Sách Vận Chuyển Và Đổi Trả Hàng
Miễn phí vận chuyển mọi đơn hàng từ 500K
- Phí ship mặc trong nước 50K
- Thời gian nhận hàng 2-3 ngày trong tuần
- Giao hàng hỏa tốc trong 24h
- Hoàn trả hàng trong 30 ngày nếu không hài lòng
Mô tả sản phẩm
Nhị thức Newton là công thức giúp khai triển lũy thừa của một tổng (a + b)n thành một đa thức. Công thức tổng quát được biểu diễn như sau: (a + b)n = Σ (nCk) * a(n-k) * bk, với k chạy từ 0 đến n, và nCk là tổ hợp chập k của n phần tử.
Công thức tổng quát và giải thích
Công thức:
(a + b)n = Σk=0n (nCk) an-k bk
Trong đó:
- n là số mũ (một số nguyên không âm).
- k là chỉ số chạy từ 0 đến n.
- nCk (đọc là "n tổ hợp k") là số tổ hợp chập k của n phần tử, được tính bằng công thức: nCk = n! / (k! * (n-k)!) với n! là giai thừa của n.
- a và b là hai số hạng trong nhị thức.
Ví dụ minh họa:
Ta muốn khai triển (x + y)3. Áp dụng công thức Nhị thức Newton:
(x + y)3 = (3C0)x3y0 + (3C1)x2y1 + (3C2)x1y2 + (3C3)x0y3
Tính các tổ hợp:
- 3C0 = 1
- 3C1 = 3
- 3C2 = 3
- 3C3 = 1
Vậy (x + y)3 = x3 + 3x2y + 3xy2 + y3
Ứng dụng của Nhị thức Newton
Công thức Nhị thức Newton có nhiều ứng dụng quan trọng trong toán học và các lĩnh vực khác như:
- Xác suất thống kê: Tính xác suất trong phân phối nhị thức.
- Giải tích: Khai triển hàm số thành chuỗi Taylor.
- Toán rời rạc: Đếm số tổ hợp và hoán vị.
- Tin học: Thuật toán và cấu trúc dữ liệu.
Tổng kết
Nhị thức Newton là một công cụ mạnh mẽ giúp đơn giản hóa việc khai triển lũy thừa của một tổng. Hiểu rõ công thức và các ứng dụng của nó sẽ giúp bạn giải quyết nhiều bài toán phức tạp trong toán học và các lĩnh vực liên quan.
Sản phẩm hữu ích: sờ ti con gái
Sản phẩm hữu ích: móng tay quặp xuống
Sản phẩm hữu ích: lời bài hát lam trường gót hồng
Xem thêm: vừa hết kinh thử que 2 vạch
Sản phẩm hữu ích: gau 5a for sale