Nguyên hàm của a mũ x
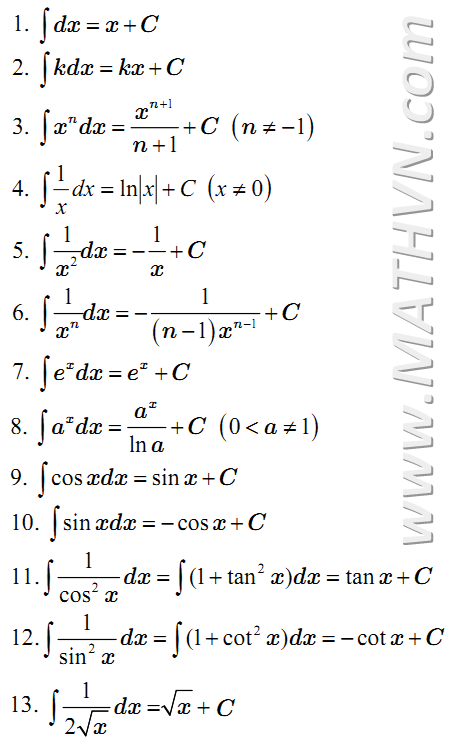

Chính Sách Vận Chuyển Và Đổi Trả Hàng
Miễn phí vận chuyển mọi đơn hàng từ 500K
- Phí ship mặc trong nước 50K
- Thời gian nhận hàng 2-3 ngày trong tuần
- Giao hàng hỏa tốc trong 24h
- Hoàn trả hàng trong 30 ngày nếu không hài lòng
Mô tả sản phẩm
Nguyên hàm của ax (với a > 0 và a ≠ 1) là ax / ln(a) + C, trong đó C là hằng số tích phân.
Công thức nguyên hàm của ax
Chứng minh công thức
Để chứng minh công thức này, ta có thể sử dụng định nghĩa của nguyên hàm. Nếu F(x) là một nguyên hàm của f(x), thì F'(x) = f(x). Hãy lấy đạo hàm của ax / ln(a):
d/dx [ax / ln(a)] = (1/ln(a)) * d/dx [ax] = (1/ln(a)) * ax * ln(a) = ax.
Như vậy, đạo hàm của ax / ln(a) là ax, chứng tỏ ax / ln(a) + C là nguyên hàm của ax.
Ví dụ áp dụng
Ví dụ 1: Tìm nguyên hàm của 2x
Áp dụng công thức, nguyên hàm của 2x là 2x / ln(2) + C.
Ví dụ 2: Tìm nguyên hàm của ex
Vì e ≈ 2.71828, và ln(e) = 1, nguyên hàm của ex là ex + C. Đây là một trường hợp đặc biệt của công thức tổng quát.
Lưu ý
Công thức này chỉ đúng khi a > 0 và a ≠ 1. Nếu a = 1, thì ax = 1, và nguyên hàm của 1 là x + C.
Xem thêm: chuyển dịch cơ cấu kinh tế theo ngành
Xem thêm: động cơ điện một chiều hoạt động dựa trên
Sản phẩm hữu ích: kí tự đặc biệt chữ trong vòng tròn
Xem thêm: các loại cây chè cà phê phù hợp với loại đất nào
Sản phẩm hữu ích: mẫu áo diều sáo đẹp