Ném ngang công thức là gì? Hướng dẫn chi tiết và ví dụ

Mô tả sản phẩm

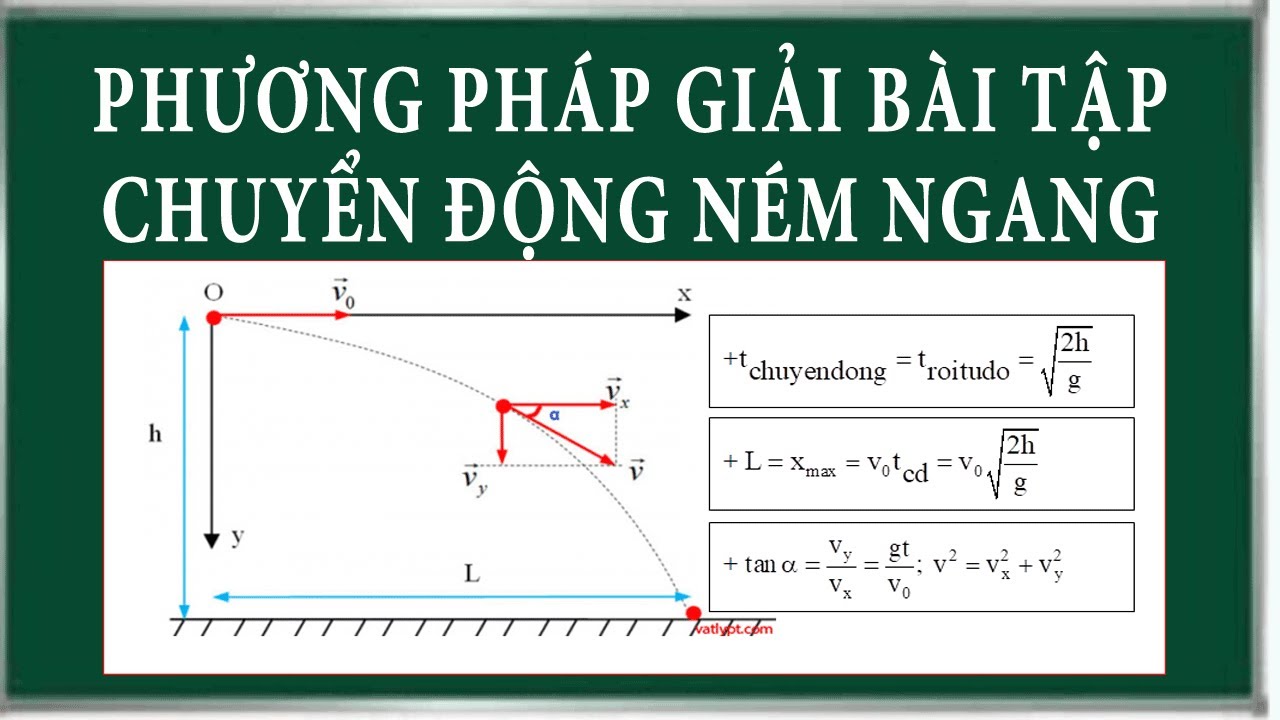
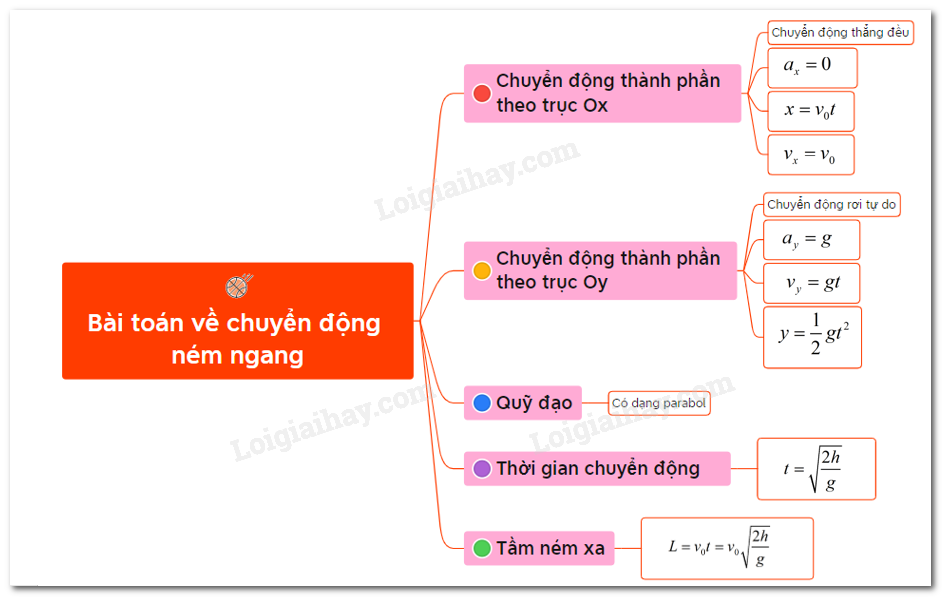
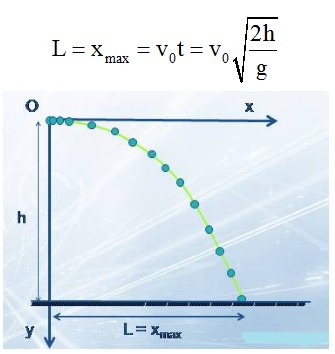
Ném ngang công thức, hay còn gọi là phương pháp ném ngang trong toán học, là kỹ thuật giải quyết các bài toán bằng cách sử dụng các phép biến đổi tương đương để đưa về dạng đơn giản hơn, dễ tính toán hơn. Nó thường được áp dụng trong giải phương trình, bất phương trình, hệ phương trình và các bài toán liên quan đến biến đổi đại số.

Các bước thực hiện ném ngang công thức

Bước 1: Nhận dạng công thức và mục tiêu

Trước khi bắt đầu, bạn cần hiểu rõ công thức ban đầu và mục tiêu mà bạn muốn đạt được. Ví dụ, nếu bạn muốn giải phương trình, mục tiêu là tìm giá trị của biến số thỏa mãn phương trình. Nếu bạn muốn rút gọn biểu thức, mục tiêu là tìm một biểu thức đơn giản hơn nhưng tương đương.

Bước 2: Áp dụng các phép biến đổi tương đương

Đây là bước quan trọng nhất. Bạn cần sử dụng các phép biến đổi đại số như cộng, trừ, nhân, chia, phân tích nhân tử, nhóm hạng tử, v.v... để biến đổi công thức ban đầu. Lưu ý rằng tất cả các phép biến đổi phải là phép biến đổi tương đương, nghĩa là không làm thay đổi tập nghiệm (hoặc tập giá trị) của công thức.

Bước 3: Kiểm tra kết quả

Sau khi đã biến đổi công thức về dạng đơn giản hơn, bạn cần kiểm tra lại kết quả bằng cách thay giá trị tìm được (nếu có) vào công thức ban đầu để xem có thỏa mãn hay không. Việc kiểm tra này giúp đảm bảo tính chính xác của kết quả.

Ví dụ minh họa

Giải phương trình: x² + 2x - 3 = 0

Ta có thể ném ngang công thức bằng cách phân tích đa thức thành nhân tử:

(x + 3)(x - 1) = 0

Từ đó, ta suy ra x = -3 hoặc x = 1.

Kiểm tra:

Với x = -3: (-3)² + 2(-3) - 3 = 9 - 6 - 3 = 0 (đúng)

Với x = 1: 1² + 2(1) - 3 = 1 + 2 - 3 = 0 (đúng)

Lưu ý khi áp dụng kỹ thuật ném ngang công thức

Kỹ thuật này đòi hỏi sự hiểu biết sâu sắc về các phép biến đổi đại số và khả năng tư duy logic. Bạn cần cẩn thận trong từng bước biến đổi để tránh sai sót. Thực hành nhiều bài tập sẽ giúp bạn thành thạo kỹ thuật này.

Sản phẩm liên quan: vật có cơ năng khi nào

Sản phẩm liên quan: giải bài đi học đều

Xem thêm: dấu hiệu nhận biết hình bình hành lớp 8

Sản phẩm hữu ích: trùng trục là gì

Sản phẩm liên quan: thỏ bông khổng lồ