Ma trận vuông cấp 3 là gì?


Chính Sách Vận Chuyển Và Đổi Trả Hàng
Miễn phí vận chuyển mọi đơn hàng từ 500K
- Phí ship mặc trong nước 50K
- Thời gian nhận hàng 2-3 ngày trong tuần
- Giao hàng hỏa tốc trong 24h
- Hoàn trả hàng trong 30 ngày nếu không hài lòng
Mô tả sản phẩm
Ma trận vuông cấp 3 là một ma trận có 3 hàng và 3 cột. Các phần tử của ma trận được sắp xếp thành một hình vuông. Nó được sử dụng rộng rãi trong toán học, đặc biệt là trong đại số tuyến tính, để biểu diễn các phép biến đổi tuyến tính và giải hệ phương trình tuyến tính.
Cấu trúc của ma trận vuông cấp 3
Các phần tử của ma trận
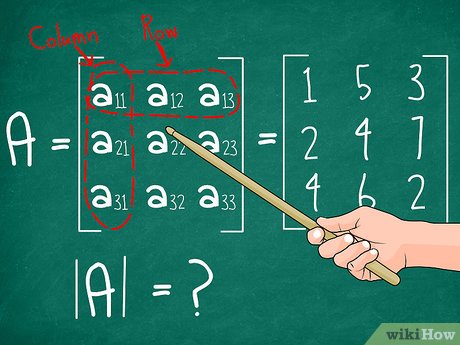
Một ma trận vuông cấp 3 được ký hiệu là A3x3 và có dạng:
A = | a11 a12 a13 |
| a21 a22 a23 |
| a31 a32 a33 |
Trong đó, aij là phần tử nằm ở hàng i và cột j của ma trận. Ví dụ, a12 là phần tử ở hàng 1 và cột 2.
Đường chéo chính
Đường chéo chính của ma trận vuông cấp 3 là đường chéo từ phần tử a11 đến a33. Tổng các phần tử trên đường chéo chính được gọi là vết của ma trận (trace).Ma trận đối xứng và ma trận chéo
Một ma trận vuông cấp 3 được gọi là đối xứng nếu aij = aji với mọi i và j. Một ma trận vuông cấp 3 được gọi là ma trận chéo nếu tất cả các phần tử ngoài đường chéo chính đều bằng 0.Ứng dụng của ma trận vuông cấp 3
Ma trận vuông cấp 3 có nhiều ứng dụng quan trọng trong nhiều lĩnh vực, bao gồm:Giải hệ phương trình tuyến tính
Ma trận vuông cấp 3 được sử dụng để biểu diễn hệ phương trình tuyến tính gồm 3 phương trình và 3 ẩn. Phương pháp Gauss-Jordan hoặc phương pháp Cramer có thể được sử dụng để giải hệ phương trình này.Biểu diễn các phép biến đổi tuyến tính
Trong hình học không gian, ma trận vuông cấp 3 có thể được sử dụng để biểu diễn các phép biến đổi tuyến tính như phép quay, phép chiếu, phép tịnh tiến...Trong đồ họa máy tính
Ma trận vuông cấp 3 được sử dụng rộng rãi trong đồ họa máy tính để thực hiện các phép biến đổi hình học như xoay, phóng to, thu nhỏ các đối tượng 3D.Trong lĩnh vực khác
Ngoài ra, ma trận vuông cấp 3 còn được ứng dụng trong các lĩnh vực khác như vật lý, kỹ thuật, kinh tế... để mô hình hóa và giải quyết các vấn đề phức tạp.Xem thêm: tiếng hót chim chìa vôi
Sản phẩm hữu ích: lời bài hát phú lê ôi đàn bà