Ma Trận Đồng Dạng Là Gì? Định Nghĩa, Tính Chất và Ứng Dụng

Mô tả sản phẩm

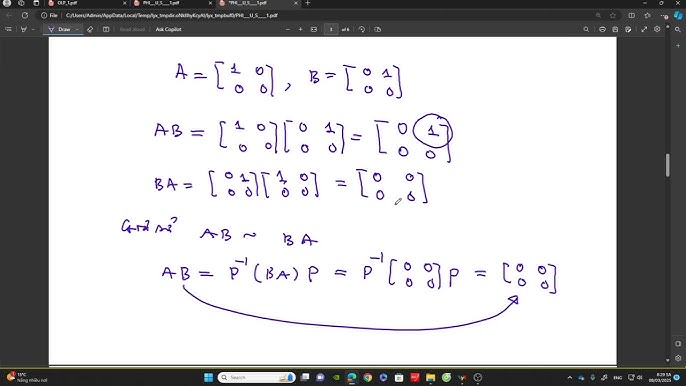
Ma trận đồng dạng là hai ma trận có cùng kích thước và biểu diễn cùng một phép biến đổi tuyến tính nhưng trong các cơ sở khác nhau. Nói cách khác, nếu hai ma trận A và B đồng dạng, thì tồn tại một ma trận khả nghịch P sao cho B = P^-1AP. Điều này có nghĩa là A và B đại diện cho cùng một phép biến đổi tuyến tính, chỉ khác nhau ở cách chọn hệ tọa độ.

Định nghĩa Ma Trận Đồng Dạng

Điều kiện cần và đủ để hai ma trận đồng dạng

Hai ma trận vuông A và B cùng cấp n được gọi là đồng dạng nếu tồn tại một ma trận khả nghịch P cấp n sao cho B = P^-1AP. Điều này là điều kiện cần và đủ để hai ma trận đồng dạng. Tính chất đồng dạng là một quan hệ tương đương, nghĩa là nó phản xạ, đối xứng và bắc cầu.

Ví dụ về ma trận đồng dạng

Giả sử A = [[1, 2], [3, 4]] và P = [[2, 0], [0, 1]]. Ta có thể tính P^-1 = [[1/2, 0], [0, 1]]. Khi đó, B = P^-1AP = [[1/2, 0], [0, 1]] [[1, 2], [3, 4]] [[2, 0], [0, 1]] = [[1, 4], [3, 4]]. Vậy A và B là hai ma trận đồng dạng.

Tính chất của Ma trận Đồng Dạng

Tính chất quan trọng của ma trận đồng dạng

Các tính chất quan trọng của ma trận đồng dạng bao gồm:

• Đường đặc trưng (đa thức đặc trưng): Hai ma trận đồng dạng có cùng đa thức đặc trưng, và do đó có cùng các giá trị riêng (eigenvalue).
• Hạng: Hai ma trận đồng dạng có cùng hạng.
• Định thức: Hai ma trận đồng dạng có cùng định thức.
• Tích vết: Hai ma trận đồng dạng có cùng tích vết (trace).

Ứng dụng của Ma trận Đồng Dạng

Ứng dụng trong giải tích tuyến tính và đại số tuyến tính

Ma trận đồng dạng có ứng dụng rộng rãi trong giải tích tuyến tính và đại số tuyến tính, đặc biệt trong việc đơn giản hóa ma trận để tính toán các giá trị riêng và vectơ riêng (eigenvector). Việc tìm kiếm ma trận đồng dạng cho phép ta chuyển đổi một bài toán phức tạp sang một bài toán đơn giản hơn, dễ tính toán hơn.

Ứng dụng trong các lĩnh vực khác

Ngoài ra, khái niệm ma trận đồng dạng còn được ứng dụng trong nhiều lĩnh vực khác như:

• Xử lý tín hiệu
• Máy học
• Vật lý
• Kỹ thuật

Sản phẩm hữu ích: những người không nên ăn củ kiệu

Xem thêm: nhẫn xoay tròn là trai hay gái

Sản phẩm hữu ích: nhận xét bài thuyết trình

Sản phẩm hữu ích: nghị luận về một bài thơ đoạn thơ lớp 9