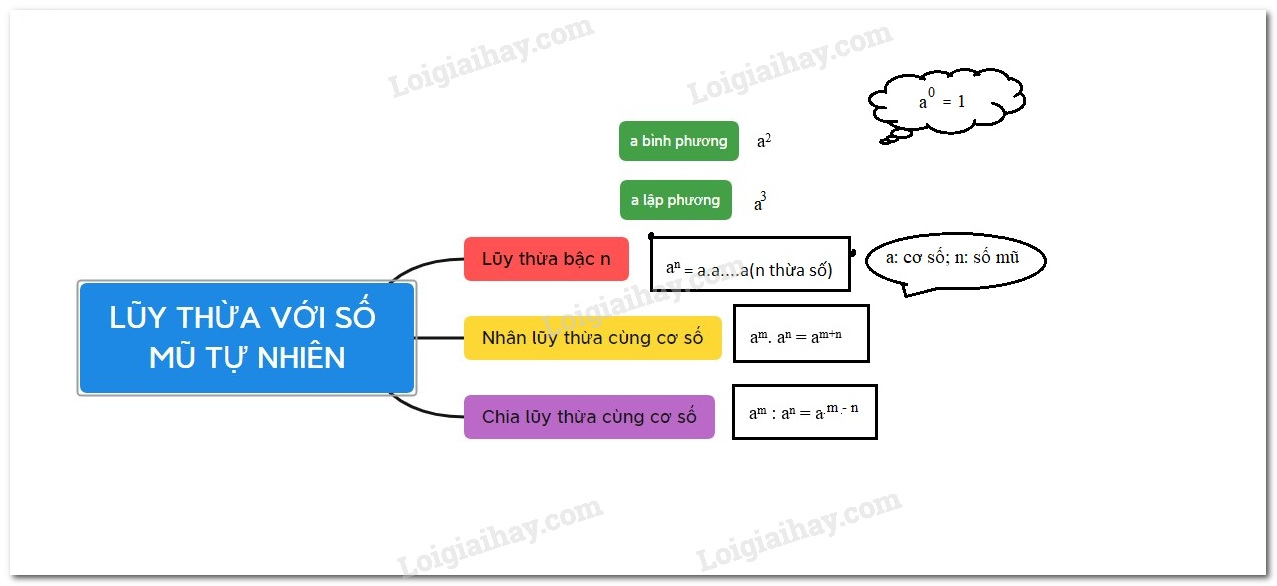
Lũy thừa với số mũ tự nhiên


Chính Sách Vận Chuyển Và Đổi Trả Hàng
Miễn phí vận chuyển mọi đơn hàng từ 500K
- Phí ship mặc trong nước 50K
- Thời gian nhận hàng 2-3 ngày trong tuần
- Giao hàng hỏa tốc trong 24h
- Hoàn trả hàng trong 30 ngày nếu không hài lòng
Mô tả sản phẩm
Lũy thừa với số mũ tự nhiên là phép toán nâng một số (cơ số) lên một lũy thừa (số mũ) là số tự nhiên. Kết quả là tích của nhiều thừa số giống nhau, mỗi thừa số bằng cơ số và số lượng thừa số bằng số mũ. Ví dụ: 2³ = 2 × 2 × 2 = 8.
Khái niệm cơ bản
Cơ số và số mũ
Trong biểu thức an, 'a' được gọi là cơ số và 'n' là số mũ. Số mũ chỉ ra số lần cơ số được nhân với chính nó. Nếu n = 0, a0 = 1 (với a ≠ 0). Nếu n = 1, a1 = a.
Tính chất của lũy thừa với số mũ tự nhiên
Lũy thừa với số mũ tự nhiên có một số tính chất quan trọng sau:
- am × an = am+n
- am : an = am-n (với a ≠ 0 và m ≥ n)
- (am)n = am×n
- (a × b)n = an × bn
- (a : b)n = an : bn (với b ≠ 0)
Ứng dụng của lũy thừa với số mũ tự nhiên
Lũy thừa với số mũ tự nhiên được ứng dụng rộng rãi trong nhiều lĩnh vực, bao gồm:
- Toán học: Tính toán, giải phương trình, chứng minh định lý.
- Khoa học: Mô tả sự tăng trưởng của quần thể, tính toán tốc độ phản ứng hóa học, tính toán năng lượng.
- Công nghệ thông tin: Mã hóa dữ liệu, xử lý hình ảnh.
- Tài chính: Tính lãi kép.
Ví dụ minh họa
Hãy tính 24:
24 = 2 × 2 × 2 × 2 = 16
Hãy tính 30:
30 = 1
Hãy tính (2 × 3)2:
(2 × 3)2 = 22 × 32 = 4 × 9 = 36
Sản phẩm liên quan: nhông công tơ mét
Xem thêm: ánh sáng trắng là tập hợp
Sản phẩm hữu ích: hình tròn ngoại tiếp tam giác
Sản phẩm liên quan: mẹ ruột của nghịch tử hào môn đã trở lại