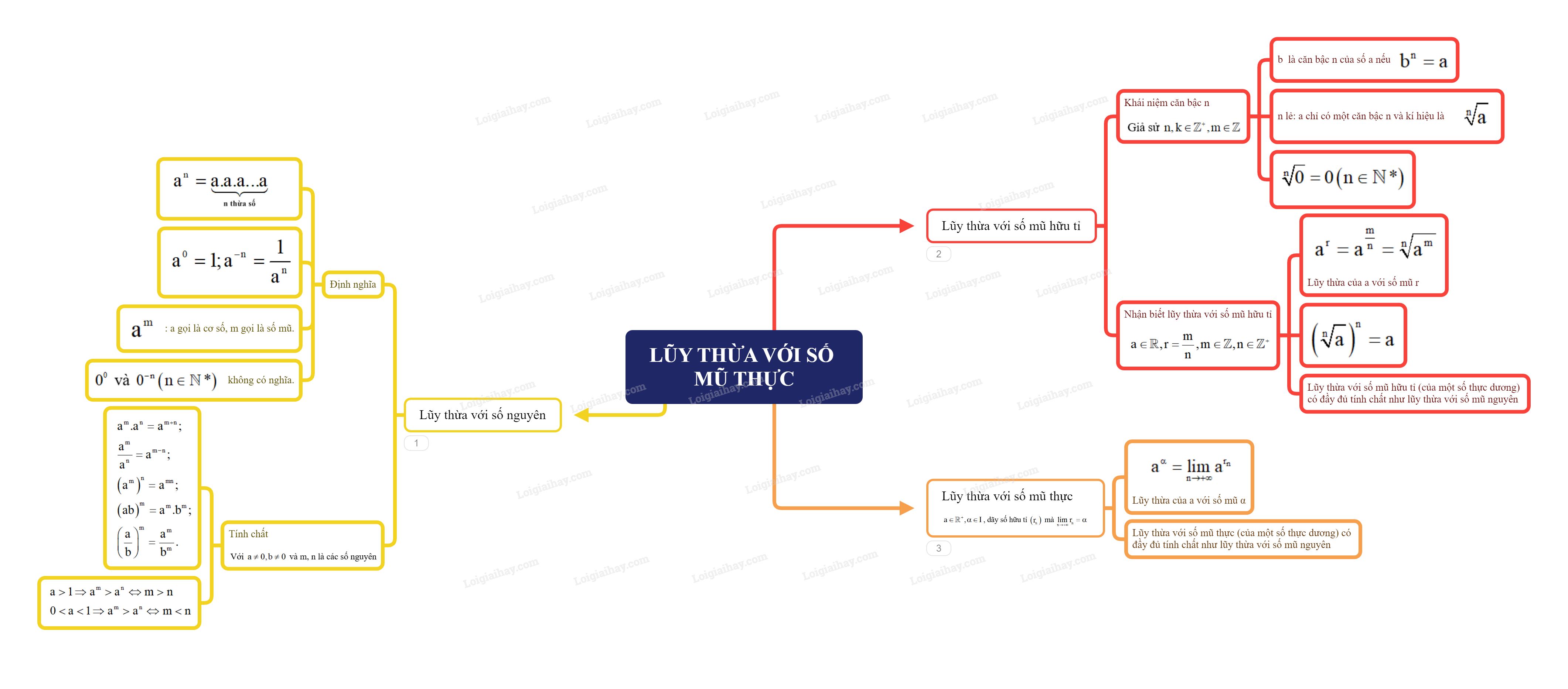
Lũy thừa với số mũ hữu tỉ

Mô tả sản phẩm

Lũy thừa với số mũ hữu tỉ là phép toán nâng một số thực a (gọi là cơ số) lên lũy thừa với số mũ là một số hữu tỉ q = m/n (với m, n là các số nguyên, n ≠ 0). Kết quả được tính bằng cách lấy căn bậc n của a mũ m, tức là a^m/n = ⁿ√(a^m). Điều kiện để phép toán này xác định phụ thuộc vào giá trị của a và n. Ví dụ: 8^2/3 = ³√(8²) = ³√64 = 4.

Định nghĩa và tính chất

Định nghĩa

Cho a là một số thực dương và q = m/n là một số hữu tỉ với m, n là các số nguyên, n > 0. Khi đó, lũy thừa với số mũ hữu tỉ a^q được định nghĩa như sau:

a^m/n = (ⁿ√a)^m = ⁿ√(a^m)

Điều kiện để định nghĩa này có nghĩa là a > 0 nếu n là số chẵn. Nếu n là số lẻ thì a có thể là số thực bất kỳ.

Tính chất

Lũy thừa với số mũ hữu tỉ thừa hưởng nhiều tính chất của lũy thừa với số mũ nguyên dương, bao gồm:

• a^m/n * a^p/q = a^{(m/n) + (p/q)}
• (a^m/n)^p/q = a^(m/n)*(p/q)
• (a*b)^m/n = a^m/n * b^m/n
• (a/b)^m/n = a^m/n / b^m/n (với b≠0)

Tuy nhiên, cần lưu ý rằng các tính chất này chỉ áp dụng khi các lũy thừa được xác định.

Ví dụ minh họa

Hãy xem xét một số ví dụ cụ thể:

• 4^3/2 = (√4)³ = 2³ = 8
• 27^2/3 = (³√27)² = 3² = 9
• 16^-3/4 = 1/(16^3/4) = 1/(√16)³ = 1/2³ = 1/8

Như vậy, việc hiểu và vận dụng được lũy thừa với số mũ hữu tỉ là rất quan trọng trong việc giải quyết các bài toán toán học, đặc biệt là trong các lĩnh vực như giải tích, đại số và hình học.

Sản phẩm hữu ích: những kim loại đứng trước hidro

Sản phẩm hữu ích: nhận biết khối cầu khối trụ

Sản phẩm liên quan: ancol nào sau đây là ancol bậc 3

Sản phẩm hữu ích: viết công thức hóa học lớp 8

Sản phẩm liên quan: phân tử khối nito