Giải phương trình log3(3x - 8) = 2 - x
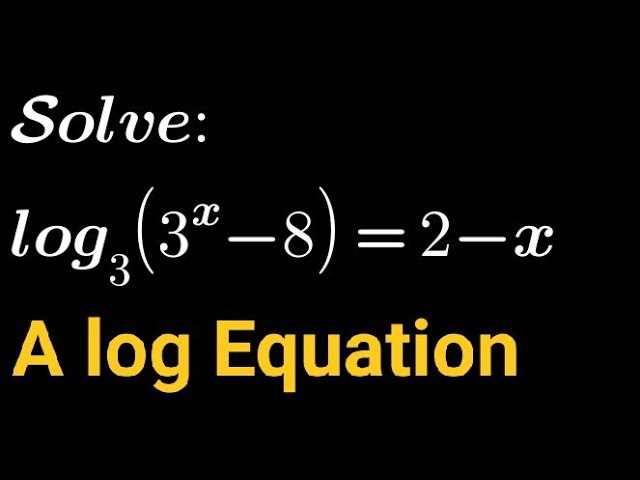
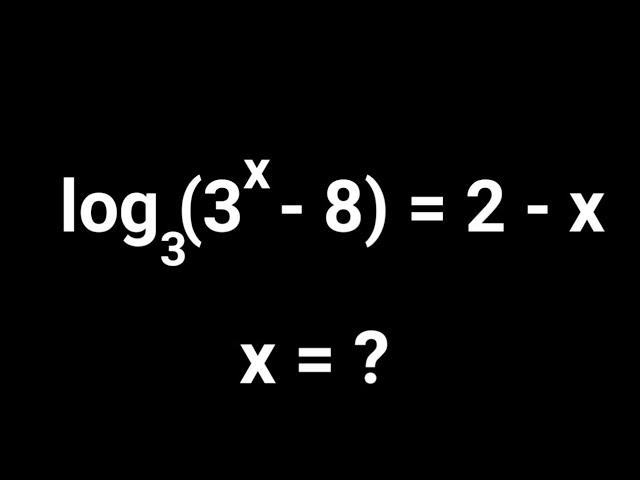
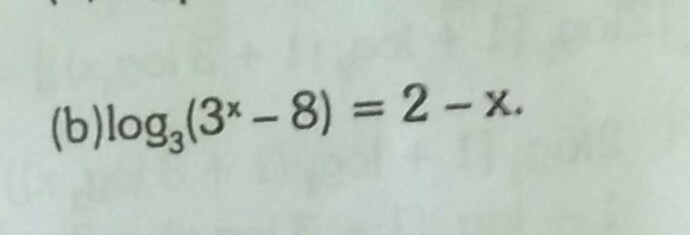
Chính Sách Vận Chuyển Và Đổi Trả Hàng
Miễn phí vận chuyển mọi đơn hàng từ 500K
- Phí ship mặc trong nước 50K
- Thời gian nhận hàng 2-3 ngày trong tuần
- Giao hàng hỏa tốc trong 24h
- Hoàn trả hàng trong 30 ngày nếu không hài lòng
Mô tả sản phẩm
Phương trình log3(3x - 8) = 2 - x có nghiệm là x = 2. Điều này có thể được kiểm chứng bằng cách thay x = 2 vào phương trình: log3(32 - 8) = log3(9 - 8) = log3(1) = 0, và 2 - x = 2 - 2 = 0. Vậy, 0 = 0, phương trình được thỏa mãn.
Phương pháp giải phương trình
Bước 1: Sử dụng định nghĩa logarit
Ta có phương trình log3(3x - 8) = 2 - x. Theo định nghĩa logarit, ta có thể viết lại phương trình này dưới dạng mũ: 3(2 - x) = 3x - 8.Bước 2: Giải phương trình mũ
Giải phương trình 3(2 - x) = 3x - 8. Ta có: 32 * 3-x = 3x - 8 9 * 3-x = 3x - 8 Đặt t = 3x (t > 0). Phương trình trở thành: 9/t = t - 8 9 = t2 - 8t t2 - 8t - 9 = 0 (t - 9)(t + 1) = 0 Vì t > 0, ta có t = 9. Do t = 3x, ta có 3x = 9 = 32. Vậy x = 2.Bước 3: Kiểm tra nghiệm
Thay x = 2 vào phương trình ban đầu: log3(32 - 8) = 2 - 2 log3(1) = 0 0 = 0 (đúng) Vậy nghiệm của phương trình là x = 2. Lưu ý rằng cần kiểm tra điều kiện xác định của logarit: 3x - 8 > 0. Với x = 2, điều kiện này được thỏa mãn.Sản phẩm hữu ích: mẫu gấu bông hot hiện nay
Sản phẩm hữu ích: nước ối như thế nào
Xem thêm: sục cu trong lớp
Sản phẩm hữu ích: ý nghĩa của bảng tuần hoàn các nguyên tố hóa học
Xem thêm: cách đuổi ốc sên