Kiến thức trọng tâm Toán lớp 11 cần nắm vững

Mô tả sản phẩm

Kiến thức trọng tâm Toán 11 bao gồm các chương về: Phép biến hình, Tổ hợp xác suất, Phương trình lượng giác, Hệ thức lượng trong tam giác, và Hình học không gian. Việc nắm vững các kiến thức này là nền tảng quan trọng cho việc học Toán ở các lớp cao hơn.

Phép biến hình trong không gian

Các phép biến hình cơ bản:

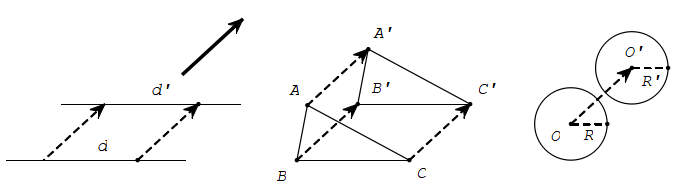
Phép tịnh tiến, phép đối xứng tâm, phép đối xứng trục, phép quay, phép vị tự được trình bày chi tiết, bao gồm cả tính chất và cách xác định ảnh của một điểm, một đường thẳng hay một hình qua các phép biến hình này. Bạn cần hiểu rõ mối liên hệ giữa các phép biến hình và cách áp dụng chúng để giải quyết các bài toán hình học.

Tổ hợp và xác suất

Quy tắc đếm cơ bản:

Hiểu rõ quy tắc cộng, quy tắc nhân, chỉnh hợp, tổ hợp và công thức tính xác suất là nền tảng quan trọng của chương này. Bạn cần luyện tập nhiều bài tập để nắm vững cách áp dụng các công thức vào các bài toán thực tiễn.

Các bài toán xác suất:

Bài toán xác suất liên quan đến biến cố, xác suất của biến cố, xác suất đầy đủ, xác suất có điều kiện… cần được làm quen và luyện tập thường xuyên để nâng cao khả năng vận dụng.

Phương trình lượng giác

Phương trình lượng giác cơ bản:

Bạn cần nắm vững các phương trình lượng giác cơ bản như sinx = a, cosx = a, tanx = a, cotx = a và cách giải chúng. Ngoài ra, cần hiểu cách giải các phương trình lượng giác phức tạp hơn bằng cách đưa về các phương trình cơ bản.

Phương trình lượng giác nâng cao:

Phương trình bậc hai đối với sinx, cosx, tanx, cotx và các phương trình lượng giác khác cần được làm quen và giải quyết nhiều để đạt được độ thành thạo cao hơn.

Hệ thức lượng trong tam giác

Định lý sin, định lý cos:

Đây là hai định lý quan trọng giúp giải các bài toán liên quan đến tính độ dài các cạnh và các góc trong tam giác. Bạn cần hiểu rõ cách áp dụng hai định lý này vào việc giải bài tập.

Diện tích tam giác:

Công thức tính diện tích tam giác bằng nhiều cách khác nhau, bao gồm công thức Heron, công thức sử dụng sin và các công thức khác cần được học thuộc và áp dụng linh hoạt.

Hình học không gian

Khái niệm cơ bản:

Bạn cần nắm vững các khái niệm cơ bản về đường thẳng, mặt phẳng, vị trí tương đối của đường thẳng và mặt phẳng trong không gian.

Các bài toán hình học không gian:

Các dạng bài toán như tính góc, tính khoảng cách giữa các đường thẳng, mặt phẳng, điểm cần được luyện tập để có khả năng tư duy không gian tốt hơn.

Sản phẩm liên quan: mơ thấy cưỡi ngựa

Sản phẩm liên quan: cách tạo nhiều folder cùng lúc

Sản phẩm hữu ích: cây lưỡi hổ tiếng anh