Khoảng Cách Từ Điểm Đến Mặt
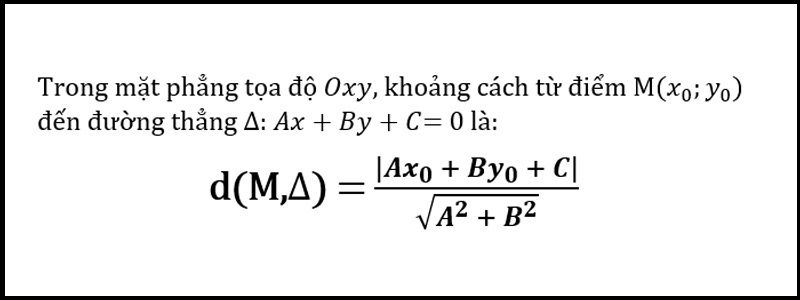
Chính Sách Vận Chuyển Và Đổi Trả Hàng
Miễn phí vận chuyển mọi đơn hàng từ 500K
- Phí ship mặc trong nước 50K
- Thời gian nhận hàng 2-3 ngày trong tuần
- Giao hàng hỏa tốc trong 24h
- Hoàn trả hàng trong 30 ngày nếu không hài lòng
Mô tả sản phẩm
Khoảng cách từ điểm đến mặt phẳng là độ dài đoạn thẳng vuông góc kẻ từ điểm đó đến mặt phẳng. Đây là khái niệm cơ bản trong hình học không gian.
Cách Tính Khoảng Cách Từ Điểm Đến Mặt Phẳng
Trong Hệ Tọa Độ Đề-các
Trong hệ tọa độ Đề-các Oxyz, cho điểm M(x0, y0, z0) và mặt phẳng (P): Ax + By + Cz + D = 0. Khoảng cách d từ điểm M đến mặt phẳng (P) được tính theo công thức:
d = |Ax0 + By0 + Cz0 + D| / √(A² + B² + C²)
Trong Hình Học Không Gian
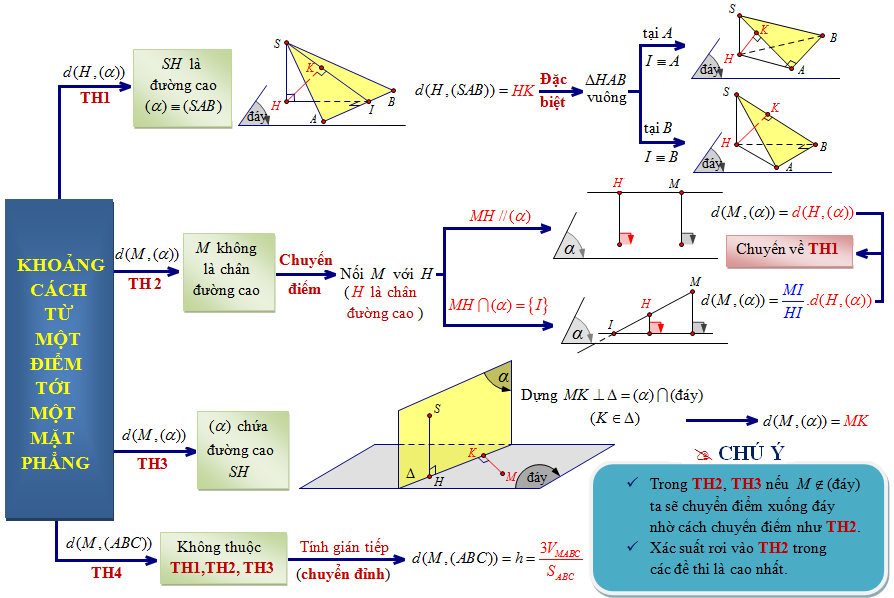
Để tính khoảng cách từ điểm M đến mặt phẳng (P) trong hình học không gian, ta cần tìm chân đường cao hạ từ M xuống (P). Đây thường là vấn đề được giải quyết bằng phương pháp hình học phẳng hoặc vectơ. Ví dụ, ta có thể tìm một đường thẳng đi qua M và vuông góc với (P), sau đó tính độ dài đoạn thẳng từ M đến giao điểm của đường thẳng đó với (P).
Ứng Dụng Của Việc Tính Khoảng Cách Từ Điểm Đến Mặt
Việc tính khoảng cách từ điểm đến mặt phẳng có ứng dụng rộng rãi trong nhiều lĩnh vực, bao gồm:
- Kiến trúc và xây dựng: Xác định khoảng cách giữa các cấu trúc, tính toán thể tích và diện tích.
- Kỹ thuật máy tính đồ họa: Xác định vị trí của các đối tượng trong không gian 3 chiều, tạo ra các hiệu ứng hình ảnh chân thực.
- Vật lý và cơ học: Tính toán lực tác động, mô phỏng chuyển động của các vật thể.
- Địa chất và khảo sát: Xác định độ sâu của các điểm dưới mặt đất.
Ví dụ Minh Họa
Cho điểm M(1, 2, 3) và mặt phẳng (P): 2x + y - 2z + 1 = 0. Khoảng cách từ M đến (P) là:
d = |2(1) + 1(2) - 2(3) + 1| / √(2² + 1² + (-2)²) = |-1| / 3 = 1/3
Xem thêm: quãng đường bằng
Sản phẩm liên quan: trạng nguyên tiếng việt lớp 1 vòng 1
Xem thêm: văn nghị luận về ô nhiễm môi trường