Hình chiếu của một điểm lên mặt phẳng


Chính Sách Vận Chuyển Và Đổi Trả Hàng
Miễn phí vận chuyển mọi đơn hàng từ 500K
- Phí ship mặc trong nước 50K
- Thời gian nhận hàng 2-3 ngày trong tuần
- Giao hàng hỏa tốc trong 24h
- Hoàn trả hàng trong 30 ngày nếu không hài lòng
Mô tả sản phẩm
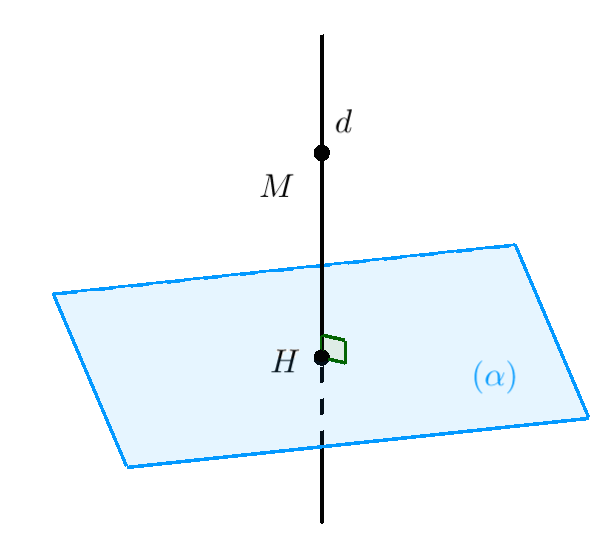
Hình chiếu của một điểm lên một mặt phẳng là điểm giao giữa mặt phẳng và đường thẳng đi qua điểm đó và vuông góc với mặt phẳng. Nói cách khác, đó là điểm trên mặt phẳng gần điểm đã cho nhất.
Xác định hình chiếu của một điểm lên mặt phẳng
Phương pháp sử dụng vector pháp tuyến
Để xác định hình chiếu H của điểm A lên mặt phẳng (P), ta cần biết tọa độ của điểm A và phương trình của mặt phẳng (P). Nếu (P) có phương trình tổng quát Ax + By + Cz + D = 0 và vector pháp tuyến của (P) là $\vec{n} = (A, B, C)$, và A có tọa độ $A(x_A, y_A, z_A)$, thì ta có thể tìm được hình chiếu H thông qua các bước sau: 1. **Viết phương trình đường thẳng d đi qua A và vuông góc với (P):** Đường thẳng d có vector chỉ phương là $\vec{n} = (A, B, C)$. Phương trình tham số của d là: x = xA + At y = yA + Bt z = zA + Ct 2. **Tìm giao điểm của d và (P):** Thay phương trình tham số của d vào phương trình của (P), ta tìm được giá trị của t. 3. **Thay giá trị t tìm được vào phương trình tham số của d:** Ta sẽ tìm được tọa độ của điểm H, chính là hình chiếu của A lên (P).Ứng dụng
Khái niệm hình chiếu của một điểm lên mặt phẳng có nhiều ứng dụng quan trọng trong: * **Hình học không gian:** Giải quyết các bài toán liên quan đến khoảng cách từ điểm đến mặt phẳng, xác định vị trí tương đối giữa điểm và mặt phẳng. * **Đồ họa máy tính:** Xây dựng các mô hình 3D, tạo hiệu ứng bóng đổ, phản chiếu. * **Kỹ thuật:** Tính toán trong lĩnh vực xây dựng, thiết kế cơ khí, ...Sản phẩm hữu ích: giải vở bài tập tiếng việt 4 chân trời sáng tạo
Sản phẩm hữu ích: công thức cấu tạo rượu etylic
Xem thêm: cách đánh dấu ngoặc vuông
Xem thêm: soạn văn 11 kết nối tri thức
Sản phẩm liên quan: bài thơ chiều hôm nhớ nhà