Hãy Sắp Xếp: Hướng Dẫn Chi Tiết về Các Phương Pháp Sắp Xếp Dữ Liệu

Mô tả sản phẩm

Hãy sắp xếp là một yêu cầu phổ biến trong nhiều lĩnh vực, từ việc sắp xếp đồ đạc trong nhà đến việc sắp xếp dữ liệu trong lập trình. Hiểu được các phương pháp sắp xếp khác nhau sẽ giúp bạn lựa chọn phương pháp tối ưu nhất cho từng trường hợp cụ thể, tiết kiệm thời gian và công sức. Bài viết này sẽ hướng dẫn chi tiết về các phương pháp sắp xếp phổ biến, cùng với ưu điểm, nhược điểm và ứng dụng thực tế của chúng.

Các Phương Pháp Sắp Xếp Cơ Bản

Sắp xếp chèn (Insertion Sort)

Sắp xếp chèn là một thuật toán sắp xếp đơn giản, hoạt động bằng cách lần lượt chèn mỗi phần tử vào đúng vị trí của nó trong một mảng đã sắp xếp một phần. Thuật toán này có hiệu suất tốt với các mảng nhỏ hoặc mảng gần như đã được sắp xếp. Tuy nhiên, với các mảng lớn, độ phức tạp thời gian của nó là O(n^2), khiến nó trở nên không hiệu quả.

Sắp xếp lựa chọn (Selection Sort)

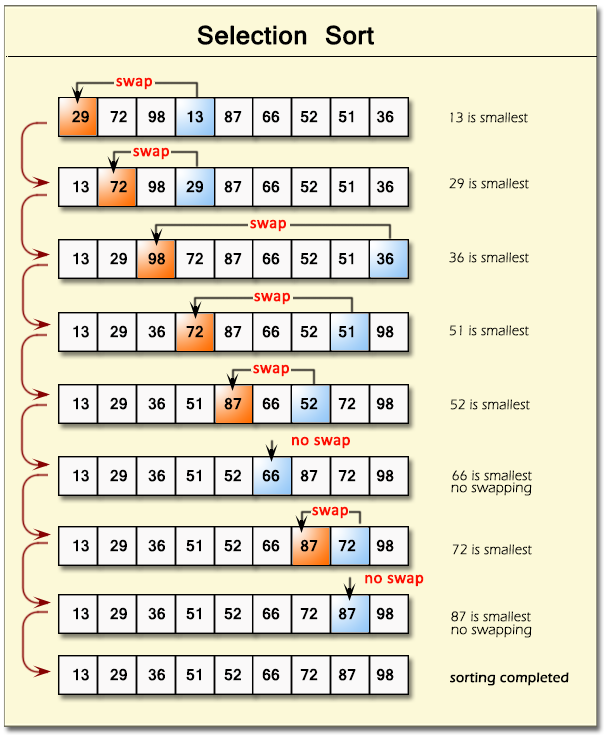
Sắp xếp lựa chọn tìm kiếm phần tử nhỏ nhất (hoặc lớn nhất) trong mảng chưa được sắp xếp và hoán đổi nó với phần tử đầu tiên của mảng chưa được sắp xếp. Quá trình này được lặp lại cho đến khi toàn bộ mảng được sắp xếp. Giống như sắp xếp chèn, sắp xếp lựa chọn cũng có độ phức tạp thời gian O(n^2), không phù hợp với các mảng lớn.

Sắp xếp nổi bọt (Bubble Sort)

Sắp xếp nổi bọt là một thuật toán sắp xếp đơn giản, lặp lại so sánh các phần tử liền kề và hoán đổi chúng nếu chúng không theo thứ tự. Quá trình này được lặp lại cho đến khi không có hoán đổi nào xảy ra. Đây là một thuật toán dễ hiểu nhưng hiệu suất khá kém với độ phức tạp thời gian O(n^2).

Các Phương Pháp Sắp Xếp Nâng Cao

Sắp xếp trộn (Merge Sort)

Sắp xếp trộn là một thuật toán sắp xếp dựa trên chia để trị (divide and conquer). Nó chia mảng thành hai nửa, sắp xếp từng nửa riêng biệt, rồi hợp nhất hai nửa đã sắp xếp lại thành một mảng đã sắp xếp. Thuật toán này có độ phức tạp thời gian O(n log n), hiệu quả hơn so với các thuật toán O(n^2) với các mảng lớn.

Sắp xếp nhanh (Quick Sort)

Sắp xếp nhanh cũng là một thuật toán dựa trên chia để trị. Nó chọn một phần tử làm phần tử trục (pivot), sau đó chia mảng thành hai phần: một phần chứa các phần tử nhỏ hơn phần tử trục và một phần chứa các phần tử lớn hơn phần tử trục. Quá trình này được lặp lại đệ quy cho đến khi mảng được sắp xếp. Trong trường hợp lý tưởng, sắp xếp nhanh có độ phức tạp thời gian O(n log n), nhưng trong trường hợp xấu nhất, nó có thể đạt O(n^2).

Sắp xếp đếm (Counting Sort)

Sắp xếp đếm là một thuật toán sắp xếp không so sánh, phù hợp với việc sắp xếp các số nguyên không âm có phạm vi giá trị nhỏ. Nó đếm số lần xuất hiện của mỗi phần tử, sau đó tạo ra mảng kết quả dựa trên số lần xuất hiện đó. Độ phức tạp thời gian của nó là O(n+k), với k là phạm vi giá trị của các phần tử.

Sắp xếp gốc (Radix Sort)

Sắp xếp gốc là một thuật toán sắp xếp không so sánh, sắp xếp các số theo từng chữ số, bắt đầu từ chữ số ít nhất có nghĩa. Nó sử dụng sắp xếp đếm cho từng chữ số. Độ phức tạp thời gian của nó là O(nk), với n là số phần tử và k là số chữ số.

Lựa Chọn Phương Pháp Sắp Xếp Phù Hợp

Việc lựa chọn phương pháp sắp xếp phù hợp phụ thuộc vào nhiều yếu tố, bao gồm kích thước của mảng dữ liệu, độ phức tạp thời gian và không gian, cũng như tính chất của dữ liệu. Với các mảng nhỏ, sắp xếp chèn hoặc sắp xếp lựa chọn có thể đủ hiệu quả. Với các mảng lớn, sắp xếp trộn hoặc sắp xếp nhanh thường là lựa chọn tốt hơn. Sắp xếp đếm và sắp xếp gốc là những lựa chọn hiệu quả khi dữ liệu có phạm vi giá trị nhỏ và được phân phối đều.

Ứng Dụng Thực Tiế

Các phương pháp sắp xếp được ứng dụng rộng rãi trong nhiều lĩnh vực, ví dụ như: * **Xử lý dữ liệu:** Sắp xếp dữ liệu theo thứ tự thời gian, giá trị, tên... để dễ dàng tìm kiếm và phân tích. * **Tìm kiếm:** Nhiều thuật toán tìm kiếm hiệu quả (như tìm kiếm nhị phân) yêu cầu dữ liệu được sắp xếp. * **Lập trình:** Sắp xếp mảng, danh sách, tập hợp dữ liệu trong các chương trình máy tính. * **Cơ sở dữ liệu:** Sắp xếp dữ liệu trong cơ sở dữ liệu để tối ưu hóa truy vấn.

Kết Luận

Hiểu rõ các phương pháp sắp xếp khác nhau là rất quan trọng để lựa chọn phương pháp tối ưu cho từng bài toán cụ thể. Việc lựa chọn đúng phương pháp không chỉ giúp tiết kiệm thời gian và công sức mà còn tối ưu hóa hiệu suất của chương trình và ứng dụng. Hy vọng bài viết này đã cung cấp cho bạn kiến thức cần thiết về các phương pháp sắp xếp và cách lựa chọn phương pháp phù hợp nhất cho nhu cầu của bạn.

Xem thêm: đi thăm lăng bác nên mặc gì

Sản phẩm liên quan: đề thi hsg văn 11

Xem thêm: giẫy dụa

Sản phẩm hữu ích: chải chiếu