Hàm số đồng biến nghịch biến lớp 11


Chính Sách Vận Chuyển Và Đổi Trả Hàng
Miễn phí vận chuyển mọi đơn hàng từ 500K
- Phí ship mặc trong nước 50K
- Thời gian nhận hàng 2-3 ngày trong tuần
- Giao hàng hỏa tốc trong 24h
- Hoàn trả hàng trong 30 ngày nếu không hài lòng
Mô tả sản phẩm
Bạn đang tìm hiểu về hàm số đồng biến và nghịch biến lớp 11? Bài viết này sẽ giúp bạn nắm vững khái niệm, điều kiện và cách xét tính đồng biến, nghịch biến của hàm số.
Khái niệm hàm số đồng biến và nghịch biến
Hàm số đồng biến
Hàm số y = f(x) xác định trên tập D được gọi là đồng biến trên D nếu với mọi x1, x2 thuộc D thỏa mãn x1 < x2, ta có f(x1) < f(x2). Nói cách khác, khi x tăng thì y cũng tăng.Hàm số nghịch biến
Hàm số y = f(x) xác định trên tập D được gọi là nghịch biến trên D nếu với mọi x1, x2 thuộc D thỏa mãn x1 < x2, ta có f(x1) > f(x2). Nói cách khác, khi x tăng thì y giảm.Điều kiện để xét tính đồng biến, nghịch biến của hàm số
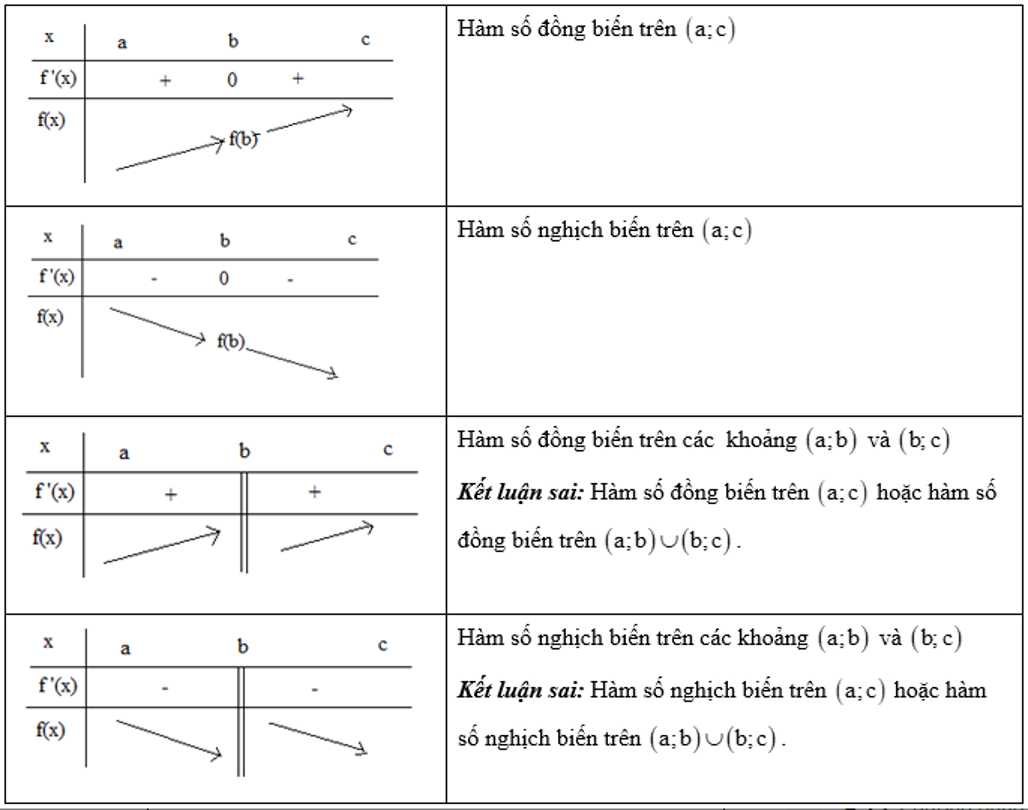
Để xét tính đồng biến, nghịch biến của hàm số, ta thường dựa vào đạo hàm của hàm số.Hàm số y = f(x) có đạo hàm trên D
+ Nếu f'(x) > 0 với mọi x thuộc D thì hàm số đồng biến trên D. + Nếu f'(x) < 0 với mọi x thuộc D thì hàm số nghịch biến trên D. + Nếu f'(x) = 0 với mọi x thuộc D thì hàm số là hàm hằng trên D (vừa đồng biến vừa nghịch biến).Lưu ý:
* Trường hợp f'(x) ≥ 0 hoặc f'(x) ≤ 0 trên D thì chưa đủ để kết luận hàm số đồng biến hoặc nghịch biến trên D. Cần phải xét thêm các trường hợp đặc biệt. * Việc xét dấu đạo hàm là rất quan trọng trong việc xác định khoảng đồng biến và nghịch biến của hàm số.Ví dụ minh họa
Xét hàm số y = x² trên khoảng (0; +∞). Ta có đạo hàm y' = 2x. Vì trên khoảng (0; +∞), y' > 0 nên hàm số đồng biến trên khoảng này.Xem thêm: bài tập am is/ are lớp 2
Sản phẩm liên quan: dấu chấm than tiếng anh là gì
Sản phẩm hữu ích: tô màu nhân vật hoạt hình
Xem thêm: chim hoa mi mai
Sản phẩm liên quan: tài liệu vật lý 11